Колесникова Елена Андреевна

1 квалификационная категория

Ростовская обл, Морозовский район, х.Костино- Быстрянский, ул. Комсомольская, д 39

МБОУ Ново- Павловская сош

Математика

« Алгебра и начала математического анализа» Алимов

Урок

10 класс

45 минут

В основе урока: технология критического мышления, технология личностно-ориентированного обучения, проблемный метод, прием « Кластер».

Конспект урока математики в 10 классе.

Тема урока: « Уравнения. Общие методы решения уравнений»

Тип урока: комбинированный.

Оборудование: презентация, раздаточный материал; ПК, тест, созданный в среде Айрен, SMART доска, КИМы по математике 2014 года.

Цели:

1. Образовательная цель: способствовать формированию у учащихся предметных компетенций

• выделить общие методы решения уравнений на примере решения иррациональных, показательных, логарифмических уравнений;

• определить насколько хорошо учащиеся умеют применять их при решении иррациональных, показательных, логарифмических уравнений;

• способствовать дальнейшему закреплению навыка учащихся в решении уравнений, использования различных языков математики (словесного, символического).

2. Развивающая цель: способствовать развитию у учащихся метапредметных компетенций:

• коммуникативных – формирование мыслительной, речевой деятельности, навыка сотрудничества;

• регулятивных – умение управлять собственной деятельностью

• развивать умение излагать материал кратко, обобщённо (в виде схем, таблиц, алгоритмов)

3. Воспитательная цель: способствовать формированию у учащихся личностных компетенций:

• смыслообразование – умение субъектного целеполагания (постановка учебных целей самим учеником, сознательно принимает решение);

• самоопределение – самооценка (оценка результатов собственной деятельности на уроке).

В основе урока: технология критического мышления, технология личностно-ориентированного обучения, проблемный метод, прием « Кластер», метод тестирования.

Ход урока

Этап 1. Вхождение (погружение) в тему урока и создание условий для осознанного нового восприятия материала.

1. Организация начала урока. ( 2 мин.)

Дидактическая задача: обеспечить нормальную внешнюю обстановку для работы на уроке, психологически подготовить учащихся к общению и предстоящему занятию.

«Дорогие друзья!

Беритесь за решение трудных математических задач! И тех, которые только что поставлены, и тех, которые уже многие десятилетия или столетия не поддаются решению.

Вас будут ожидать страдания, вы будете разочарованы, когда вам будет казаться, что вы напрасно потратили годы на поиски ускользающего призрака. Все может быть.

Но вы будете сторицей вознаграждены, когда в один прекрасный день окажетесь перед той заветной целью, к которой так долго и так трудно шли.

Не будьте безучастными и равнодушными, в противном случае это будет духовная смерть»

Я начала наш урок словами Данте о беспредельной жажде познания, с которой должен жить человек.

Вам, учащимся 10-го класса скоро предстоит переступить школьный порог и столкнуться с широким кругом жизненных проблем, жизненных задач. Г. Галилей сказал когда-то: «Нельзя чему-нибудь научить человека, можно только помочь ему обнаружить это внутри себя». Сегодня я попробую создать для вас условия «подлинной жизни на уроке». Читая задачу, попытайтесь, по возможности, представить себя в сюжете задачи. Уберите мысленно психологический барьер, мешающий вам взяться за ее решение.

2. Целеполагание

Дидактическая задача: организовать и целенаправить познавательную деятельность учащихся, подготовить их к усвоению нового материала. Учить учащихся формулировать цели учения и выбирать конкретные средства для их достижения.

-Знакомы ли Вам, записанные равенства?

-Какие это уравнения?

- Ребята, поясните, пожалуйста, смысл словосочетаний «методы решения уравнений», «общие методы решения уравнений».

Предполагаемые ответы учащихся:

• Методы решения уравнений – это способы, приемы, с помощью которых можно решить то или иное уравнение.

• Общие методы решения уравнений – это такие способы, приемы, с помощью которых можно решить  уравнения разного типа.

-Сформулируйте тему урока.

- В соответствии с темой урока, сформулируйте задачи и цели, используя опорные слова:

вспомнить →виды уравнений, какие методы решения уравнений  нам известны.

узнать → общие методы решения уравнений.

научиться → учиться применять их при решении уравнений разного типа, проверить насколько хорошо мы ими владеем.

Этап 2. Организация и самоорганизация учащихся в ходе дальнейшего повторения и обобщения материала. Организация обратной связи.

Дидактическая задача: дать учащимся конкретное представление об основной идее изучаемого вопроса.

-   Где вам могут пригодиться эти знания? ( При написании ЕГЭ)

- Этот урок будем рассматривать как фрагмент подготовки к ЕГЭ. Знаете ли вы, какое задание ЕГЭ проверяет знания в области решения уравнений?(В 5)

Индивидуальное задание паре учащихся: просмотрите демоверсию ЕГЭ, варианты предложенных КИМов, какие виды уравнений необходимо рассмотреть для успешного выполнения задания В-5?

Задание для работы в паре.

Учащимся предлагается составить кластер по теме «Уравнения». На столах у каждого находится лист (формат А 4).
На листе делается посередине надпись «Уравнения». Затем учащимся предлагается слева записать виды уравнений, а справа способы их решения.

REM: Кластер-  

      выделение смысловых единиц текста и графическое оформление в определенном порядке в виде грозди .

Одному обучающемуся можно предложить это задание выполнить на доске.( Возможно применение SMART доски, чтобы в процессе обсуждения кластера была возможность дополнения и корректировки). Затем групповое обсуждение полученного кластера. Корректировка кластера.

- Вы только что попытались установить связи между видами уравнений, формулами и способами их решения. Сравните свою работу с модельным ответом.

-Какие способы Вы отнесете к общим способам решения уравнений?

Предполагаемый ответ уч-ся:

1. Метод разложения на множители.

2. Метод введения новой переменной.

3. Метод замены уравнения равносильным.

В случае затруднения обратиться к заготовкам приложений « Способы решения иррациональных, логарифмических и показательных уравнений»

Индивидуальные листы:

Приложение 1:Методы решения иррациональных уравнений

1. Замена равносильным

Возведем обе части уравнения в квадрат

Решая данное квадратное уравнение, находим

Проверка корней.

1) Если х = 42, то 2) Если х = 2, то

Значит, число 2 является

корнем уравнения.

Значит, число 42 не является

корнем уравнения.

Ответ. 2

II. Способ

Ответ. 2

2. Разложение на множители

Числа -2 и 2 посторонние корни, т.к. не удовлетворяют условию х ≥ 3.

Ответ.3

3. Введение новой переменной

ОДЗ: х – любое число.

Пусть где t ≥ 0, тогда исходное уравнение примет вид

Решая данное квадратное уравнение, находим, что

Число – 7 посторонний корень, т.к. не удовлетворяет условию t ≥ 0.

Если t = 6, то

Решая данное уравнение, находим

Ответ. х= - 4,5; х = 3.

Методы решения логарифмических уравнений

1. Введение новой переменной

ОДЗ: х>0. Пусть , тогда уравнение примет вид

Решив данное квадратное уравнение, находим его корни

Следовательно,

Ответ. х = 10; х = 100.

2. Замена уравнения равносильным

Решая квадратное уравнение находим,

Корень х = - 4, не удовлетворяет условию

Ответ. 0

3. Разложение на множители

Ответ. 2; 3

Методы решения показательных уравнений

1. Замена уравнения равносильным

Ответ. – 3

2. Введение новой переменной

Пусть где тогда уравнение примет вид

Решая данное квадратное уравнение, находим, что

Корень не удовлетворяет условию

Следовательно, решим уравнение

Ответ. x= 3.

3. Разложение на множители

Запишем в рабочих тетрадях опорный конспек-слайд7.

(Дать печатный вариант каждому в целях экономии времени)

1. Метод разложения на множители.

Уравнение f(x)g(x)h(x)=0 заменить совокупностью уравнений f(x)=0, g(x)=0, h(x)=0. Необходима проверка корней.

2. Метод введения новой переменной.

Пусть g(x)=t,  тогда уравнение p(g(x))=0 равносильно уравнению p(t)=0.

3. Метод замены уравнения равносильным.

1. При решении показательных уравнений: уравнение a^f(x) = a^g(x) (a >0, a≠1) равносильно  f(x) = g(x).

2. При решении логарифмических уравнений: уравнение log_a f(x) = log_a g(x) (f(x) > 0, g(x)>0,  a>0,  a≠1) равносильно f (x) = g(x).

3. При решении иррациональных уравнений (можно применять, если функции монотонны): уравнение   равносильно f(x) = g(x).

-Как же правильно выбрать тот или иной способ решения уравнений?

Предполагаемый ответ: нужно определить вид этого уравнения.

Предлагаю во время самостоятельной работы пользоваться «Схемой решения проблемы»

(Слайд 8 «Схема решения проблемы»)

- осознание проблемы;

- постановка цели;

- формирование задач;

- выбор стратегии;

- планирование;

- контроль выполнения плана;

- осознание результата деятельности

Работа в парах: каждой паре предлагаю решить одно из уравнений, оформить решение на доске, ответ прокомментировать.

Задания парам:

1 пара
2 пара	;
3 пара	log(x-2)=2, lg (x2 + 1) = 1; lg ( х + 7 ) – lg ( х + 5 ) = 1

Этап 3. Деятельность учащихся по самостоятельному применению знаний и умений при решении заданий В-5.

Индивидуальная работа учащихся на ПК. Выполнение теста, созданного в среде Айрен .Тест содержит 10 уравнений различных видов, после прохождения теста каждый учащийся получает отметку за урок и имеет возможность ознакомиться со своими результатами.

Этап 4. Подведение итогов, рефлексия.

– Что дал ВАМ прием «Кластер»?
- В результате работы на уроке мы получили в некотором роде опорный конспект для решения уравнений В-5 задания. Он поможет вам справиться с домашним заданием.

Работа по закреплению данной темы будет продолжаться, так как в нашем кластере остались не заполненные места и вопросы ( вам предстоит изучение тригонометрических уравнений)
– Имеет ли практическое значение данная тема?

А сейчас предлагаю Вам в парах составить « Синквейн» по теме « Уравнения».

Представление каждым своей работы.

Этап 5. Домашнее задание.

Индивидуальные листы каждому из учащихся (задания из ОБЗ).

Этап 6. Заключение.

Завтра вам придется принимать решения в реальной жизни. Вам пригодятся те качества, которые вы продемонстрировали на уроке: мобильность и креативность, способность применять свои знания на практике и умение мыслить нестандартно. Вот тогда оценку за правильно решенную задачу вам поставит уже сама жизнь.

Накопительная папка ученика: задание В-5

Кластер по теме « Уравнения»

Уравнения

показа

тельные

1.Формулы.

2. Разложение на множите

ли.

3.Теорема, обратная т. Виета.

4. Введение новой переменной

(биквадрат

ные)

Приложение 1:Методы решения иррациональных уравнений

1. Замена равносильным

Возведем обе части уравнения в квадрат

Решая данное квадратное уравнение, находим:

Проверка корней.

1) Если х = 42, то 2) Если х = 2, то

Значит, число 2 является

корнем ур-я

Значит, число 42 не является

корнем уравнения.

Ответ. 2

II. Способ

Ответ. 2

2. Разложение на множители

Числа -2 и 2 посторонние корни, т.к. не удовлетворяют условию х ≥ 3.

Ответ.3

3. Введение новой переменной

ОДЗ: х – любое число.

Пусть где t ≥ 0, тогда исходное уравнение примет вид

Решая данное квадратное уравнение, находим, что

Число – 7 посторонний корень, т.к. не удовлетворяет условию t ≥ 0.

Если t = 6, то

Решая данное уравнение, находим

Ответ. х= - 4,5; х = 3.

Методы решения логарифмических уравнений

1. Введение новой переменной

ОДЗ: х>0. Пусть , тогда уравнение примет вид

Решив данное квадратное уравнение, находим его корни

Следовательно,

Ответ. х = 10; х = 100.

2. Замена уравнения равносильным

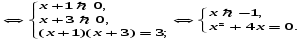
Решая квадратное уравнение находим,

Корень х = - 4, не удовлетворяет условию

Ответ. 0

3. Разложение на множители

Ответ. 2; 3

Методы решения показательных уравнений

1. Замена уравнения равносильным

Ответ. – 3

2. Введение новой переменной

Пусть где тогда уравнение примет вид

Решая данное квадратное уравнение, находим, что

Корень не удовлетворяет условию

Следовательно, решим уравнение

Ответ. x= 3.

3. Разложение на множители

Общие методы решения уравнений

1. Метод разложения на множители.

Уравнение f(x)g(x)h(x)=0 заменить совокупностью уравнений f(x)=0, g(x)=0, h(x)=0. Необходима проверка корней.

2. Метод введения новой переменной.

Пусть g(x)=t,  тогда уравнение p(g(x))=0 равносильно уравнению p(t)=0.

3. Метод замены уравнения равносильным.

1. При решении показательных уравнений: уравнение a^f(x) = a^g(x) (a >0, a≠1) равносильно  f(x) = g(x).

2. При решении логарифмических уравнений: уравнение log_a f(x) = log_a g(x) (f(x) > 0, g(x)>0,  a>0,  a≠1) равносильно f (x) = g(x).

3. При решении иррациональных уравнений (можно применять, если функции монотонны): уравнение   равносильно f(x) = g(x).

-Как же правильно выбрать тот или иной способ решения уравнений?

Технологическая карта урока