Бюджетное общеобразовательное учреждение Омской области города Калачинска «Гимназия №1»

Международный конкурс-фестиваль педагогического мастерства

«Педагогическая академия: МАСТЕРство И инновациЯ»

Номинация «Конкурс авторских программ»

Тема работы

«Программа

краткосрочного курса внеурочной деятельности

«Математика в шпаргалках»

	Автор: Коновалова Тамара Владимировна должность: учитель начальных классов преподаваемый предмет: начальные классы телефон 89050991578 Адрес электронной почты: sitnikovatv@mail.ru

город Калачинск - 2020

Рабочая программа

краткосрочного курса внеурочной деятельности

«Математика в шпаргалках»

для 4 класса

Автор программы:

Коновалова Тамара Владимировна,

учитель начальных классов

БОУ г. Калачинска «Гимназия №1»

Пояснительная записка

Программа курса внеурочной деятельности «Математика в шпаргалках» предназначена для проработки типичных проблем в освоении математики обучающимися начальных классов.

В 4 классе обучающиеся выполняют Всероссийские проверочные работы, в том числе и по математике. Согласно обзорному анализу результатов Всероссийских проверочных работ в 2019 году на территории Омской области основные затруднения у обучающихся 4 класса при выполнении ВПР по математике возникли в задании № 12.

Задание № 12 – направлено на оценку умения владеть основами логического и алгоритмического мышления (решать задачи в 3-4 действия).

Цель программы: формирование умения применять алгоритмы решения логических задач, различных типов задач в 3-4 действия

Задачи:

1. Развивать умение анализировать, отбирать, интерпретировать информацию из текста задачи.

2. Развивать интеллектуальные способности обучающихся до уровня понимания причинно-следственных связей.

3. Формировать умение ориентироваться в разнообразии способов решения задач.

Общая характеристика программы

Программа рассчитана на 8 часов.

Целевая аудитория: обучающиеся 4 класса, испытывающие трудности в выборе способа решения задач по математике, применении алгоритма решения задач.

Рабочая программа реализует следующие направления внеурочной деятельности: общеинтеллектуальное, общекультурное.

Результаты освоения курса внеурочной деятельности

Личностные результаты:

- развитие мотивов учебной деятельности и формирование личностного смысла учения;

- развитие навыков сотрудничества со взрослыми и сверстниками в разных учебных ситуациях.

Метапредметные результаты

Регулятивные универсальные учебные действия:

- овладение способностью принимать и сохранять цели и задачи учебной деятельности, поиска средств ее осуществления;

- формирование умения планировать, контролировать и оценивать учебные действия в соответствии с поставленной задачей и условиями ее реализации; определять наиболее эффективные способы достижения результата;

- формирование умения понимать причины успеха/неуспеха учебной деятельности и способности конструктивно действовать даже в ситуациях неуспеха;

- освоение начальных форм познавательной и личностной рефлексии.

Познавательные универсальные учебные действия:

- освоение способов решения проблем поискового характера;

- овладение логическими действиями сравнения, анализа, синтеза, обобщения, классификации по родовидовым признакам, установления аналогий и причинно-следственных связей, построения рассуждений, отнесения к известным понятиям;

- овладение базовыми предметными и межпредметными понятиями, отражающими существенные связи и отношения между объектами и процессами;

- умение работать в информационной среде.

Коммуникативные универсальные учебные действия:

- готовность слушать собеседника и вести диалог;

- готовность признавать возможность существования различных точек зрения и права каждого иметь свою;

- излагать свое мнение и аргументировать свою точку зрения и оценку событий.

Содержание курса внеурочной деятельности

с указанием форм организации и видов деятельности

Занятие № 1

Работаем с текстом задачи. Составляем шпаргалки по математике. Преобразование, интерпретация, применение информации текста задачи. Сравнение объектов текста задачи. Цветная маркировка текста задачи. Выводы, аргументы, сопоставление информации из разных задач. Задачи, выраженные в косвенной форме.

Виды деятельности: решение задач, выраженных в косвенной форме, составление алгоритма решения задач данного вида.

Форма организации деятельности: практикум

Занятие №2

Работаем с таблицами, схемами и рисунками. Составляем шпаргалки по математике. Решение табличных, графических задач. Представление текста задачи в виде рисунка, схематического рисунка, схематического чертежа, краткой записи, в таблице, на диаграмме. Задачи геометрического содержания.

Виды деятельности: решение геометрических задач, анализ таблиц, схем, составление схематического чертежа, диаграммы, таблицы

Форма организации деятельности: практикум

Занятия № 3 - 4

Решаем текстовые задачи. Составляем шпаргалки по математике. Текстовые задачи, содержащие величины, характеризующие процесс движения (скорость, время, пройденный путь), расчёт стоимости товара (цена, количество, общая стоимость товара), расход материала при изготовлении предметов (расход на один предмет, количество предметов, общий расход). Задачи на определение начала, конца и продолжительности события. Задачи на нахождение доли целого и целого по его доле.

Виды деятельности: решение задач на расчёт стоимости товара, на нахождение доли целого и целого по его доле, на движение, составление памяток, картинных правил

Форма организации деятельности: практикум

Занятия №5 - 6

Решаем логические задачи. Составляем шпаргалки по математике. Задачи с палочками. Магические квадраты. Задачи на составление маршрутов. Задачи на взвешивание. Задачи на переливание.

Виды деятельности: решение логических задач, составление опорных схем, моделирование

Форма организации деятельности: практикум

Занятие №7

Играем в математические игры. «Математический ринг», «Исправь ошибку», «Математическое лото», «Лабиринт». Проект «Математическая игра»

Виды деятельности: определение темы проекта, постановка цели, анализ информации о математических играх, составление плана реализации проекта, выполнение плана проекта, презентация игры, анализ результатов проекта.

Формы организации деятельности: игра, проект

Занятие №8

«Проверь себя». Решение разных типов задач по математике.

Виды деятельности: контроль знаний

Формы организации деятельности: работа с интерактивными тренажерами

Тематическое планирование

№ п/п	Тема занятий	Количество часов
1	Работаем с текстом задачи. Составляем шпаргалки по математике	1
2	Работаем с таблицами, схемами и рисунками. Составляем шпаргалки по математике	1
3	Решаем текстовые задачи. Составляем шпаргалки по математике	1
4	Решаем текстовые задачи. Составляем шпаргалки по математике	1
5	Решаем логические задачи. Составляем шпаргалки по математике	1
6	Решаем логические задачи. Составляем шпаргалки по математике	1
7	Играем в математические игры. Проект «Математическая игра»	1
8	Проверь себя	1
Итого: 8 часов

Описание учебно-методического обеспечения программы

Перечень методической литературы

1. Воронцов А.Б., Заславский В.М. Сборник проектных задач. Начальная школа. Пособие для учителей общеобразовательных учреждений. - Москва: Просвещение, 2012

2. Гейдман Б.П. Подготовка к математической олимпиаде. Начальная школа. – Москва: Айрис- пресс, 2016

3. Горев П.М., Утёмов В.В. Значимые события в жизни Совёнка. Учебно-методическое пособие. - Киров: МЦИТО, 2016

4. Горев П.М., Утёмов В.В. Креативное лето с Совёнком. Учебно-методическое пособие. - Киров: МЦИТО, 2017

5. Горев П.М., Утёмов В.В. Летнее расследование Совёнка. Учебно-методическое пособие. - Киров: МЦИТО, 2014

6. Логические задания для 1-2 класса: орешки для ума/сост. И.В. Ефимова. – Ростов-на-Дону: Феникс, 2016

7. Логические задания для 3 класса: орешки для ума/сост. И.В. Ефимова. – Ростов-на-Дону: Феникс, 2014

8. Логические задания для 4 класса: орешки для ума/сост. И.В. Ефимова. – Ростов-на-Дону: Феникс, 2016

9. Мельникова Т.А., Чермашенцева О.В. Математика. Развитие логического мышления. 1-4 классы. Комплекс упражнений и задач. ФГОС. – Волгоград: Учитель, 2015

10. Мохначёва Г.И. Русский язык. 4 класс. Тетрадь для победителя. Готовимся к олимпиаде.– Мозырь: Белый ветер, 2015

11. Мохначёва Г.И. Математика. 4 класс. Готовимся к олимпиаде. Часть 2.– Мозырь: Белый ветер, 2015

12. Феоктистова В.Ф. Исследовательская и проектная деятельность младших школьников. Рекомендации, проекты. ФГОС. - Волгоград: Учитель, 2015

13. Хиленко Т.П. Типовые задачи по формированию УУД. Работа с информацией. 4 класс. – М.: Просвещение, 2016.образовательную деятельность. В 2 ч. – М.: Баласс, 2015.

ЭОР

1. Полезные уроки. Русский язык за 10 минут в день. 4 класс (CDpc). Издательство: 1С, 2012 г.

2. Математика. 4 класс. Часть 1 (CD). Издательство: «Экзамен», 2014 г.

3. Математика. 4 класс. Часть 2 (CD) Издательство: «Экзамен», 2014 г.

4. Полезные уроки. Математика за 10 минут в день. 3 класс (CDpc). Издательство: 1С, 2012 г.

Интернет – ресурсы

МетаШкола https://metaschool.ru/

Кенгуру http://www.kenguru.sp.ru/club1.html

Математика - онлайн http://www.math-on-line.com/

Данетки – форум эрудитов http://eruditov.net/forum/36

Учи. ру https://uchi.ru/teachers/stats/main

Учимся решать задачи https://luckclub.ru/kak-nauchit-rebenka-reshat-zadachi-4-klass-raznymi-sposobami-logicheskie-zadachi-na-skorost-na-vremya-vzaimosvyazannye-zadachi-kak-nauchitsya-reshat-zadachi-4-klass

Приложение № 1

Текстовые задачи

Задача 1

Сколько листов бумаги, купил каждый из трех учителей, если у одного 23 учеников, у другого 27 учеников, у третьего 30 учеников? Всего тремя учителями было куплено 480 листов бумаги, на каждого ученика равное количество листов. Выбери верный ответ:

Решение:

1) 23 + 27 + 30 = 80 (всего учеников)

2) 480 : 80 = 6 (листов бумаги каждому ученику)

3) 23 * 6 = 138

4) 27 * 6 = 162

5) 30 * 6 = 180

Ответ: б) 138, 162, 180.

Задача 2

У одного угря 116 позвонков. Сколько позвонков у акулы, если у 6 акул и 4 угрей 2840 позвонков? Укажи верный ответ:

Решение:

1) 116 * 4 = 464 (позвонков у 4 угрей)

2) 2840 - 464 = 2376 (позвонков у 6 акул)

3) 2376 : 6 = 396 (позвонков у 1 акулы)

Ответ: б) 396.

Задача 3

Производительность машины для изготовления бутылок - 16 бутылок за 2 минуты. Какая производительность машины будет в сутки? Укажи верный ответ:

а) 2384;

6) 11520;

в) 176;

г) 282.

Решение:

1) 16 : 2 = 8 (бутылок в минуту)

2) 8 * 60 = 480 (бутылок в час)

3) 480 * 24 = 11520 (бутылок в сутки)

Ответ: 6) 11520.

Задача 4

На ремонт школы нужно 120 банок белой и коричневой краски. По 2 банки белой и 4 коричневой для каждого класса. Сколько банок каждой краски было куплено? Укажи верный ответ:

Решение:

1) 2 + 4 = 6 (белой и коричневой краски на класс)

2) 120 : 6 = 20 (классов в школе)

3) 2 * 20 = 40 (банок белой краски купили)

4) 4 * 20 = 80 (банок коричневой краски купили)

Ответ: б) 80 и 40.

Задача 5

В магазине за 5 норковых шуб нужно заплатить 312 500 руб., а шуба из песца стоит 17 500. Сколько будут стоить 8 песцовых шуб и 3 норковые.

Решение:

1) 312 500 : 5 = 62500 (стоит одна норковая шуба)

2) 8 * 17500 = 140 000 (стоят 8 песцовых шуб)

3) 3 * 62500 = 187 500 (стоят 3 норковые шубы)

4) 187500 + 140000 = 327 500

Ответ: б) 327 500 руб.

Задача 6

На шапку и одну пару перчаток пошло 300 грамм пряжи. Сколько пряжи пошло на каждую перчатку, если на шапку пошло 180 грам пряжи?

Решение:

1) 300 - 180 = 120 (пряжи пошло на 2 перчатки)

2) 120 : 2 = 60 (пряжи пошло на 1 перчатку)

Ответ: г) 60 г.

Задача 5

Сколько ткани понадобится для изготовления 9 курток, если на 19 курток нужно 38 метров ткани.

Решение:

1) 38 : 19 = 2 (метра ткани на 1 куртку)

2) 2 * 9 = 18 (метров ткани на 9 курток)

Ответ: в) 18 м.

Задача 6

Полоску бумаги разрезали на три части. После этого самую большую из полученных частей снова разрезали на три части. Затем снова самую

большую из полученных частей разрезали на три части. Так поступили много раз: на каждом шаге самую большую часть разрезали на три части. Могло ли в итоге получиться 100 частей?

Решение

Получается последовательность, в которой первое число равно 2 (третью бумажку разрываем), а каждое следующее число будет на 2 больше предыдущего, кроме последнего. При последнем разрезании бумаги получится 3 кусочка. Получится нечетное количество кусочков, которое не делится на 2, а число 100 на 2 делиться, значит в итоге получится 100 не может.

Ответ

Нет, не может получится 100 частей.

Задача 7

Ира вырезала из бумаги несколько пятиугольников и шестиугольников. Всего у вырезанных фигурок 38 вершин. Сколько пятиугольников вырезала Ира?

Ответ 2

Задача 8

Каков периметр синей фигуры?

Ответ: Здесь есть два квадрата, у которых есть общая часть стороны. Так как сторона квадрата равна 10 см и часть стороны равна 8 см, то общая часть 2 см, а оставшаяся часть второго квадрата равна 8 см. Периметр равен 10 + 10 + 8 + 10 + 10 + 10 + 8 + 10 = 76 см.

Задача 9

Сторона квадрата 6 см. Найди длину прямоугольника с таким же периметром и шириной 3 см.

Решение:

6 · 4 = 24 (см) -находим периметр квадрата

3 + 3 = 6 (см) -сумма ширины прямоугольника

24 — 6 = 18 (см)- сумма двух длин прямоугольника

18 : 2 = 9 (см)

Ответ: Длина прямоугольника 9 см.

Задача 10

Сторона клумбы квадратной формы 8 м. 7/16 всей площади клумбы засажено ромашками, а остальная площадь – незабудками. На какой площади клумбы посажены незабудки? Решение:

1) 8 ∙ 8 = 64 (площадь клумбы)

2) 64 : 16 = 4(1/16 клумбы)

3) 4 ∙ 7 = 28 (площадь клумбы, засаженная ромашками)

4) 64 – 28 = 36

Ответ: Незабудками засажено 36 м².

Задача 11

Однажды Винни-Пух захотел полакомиться медом и пошел к пчелам в гости. По дороге нарвал букет цветов, чтобы подарить труженицам пчелкам. Пчелки очень обрадовались, увидев мишку с букетом цветов, и сказали: «У нас есть большая бочка с медом. Мы дадим тебе меда, если ты сможешь с помощью двух сосудов вместимостью 3 л и 5 л налить себе 4 л!» Винни-Пух долго думал, но все-таки смог решить задачку. Как он это сделал? 

Решение:

Как в результате можно получить 4 л? Нужно из 5-литрового сосуда отлить 1 л. А как это сделать? Нужно в 3-литровом сосуде иметь ровно 2 л. Как их получить? – Из 5-литрового сосуда отлить 3 л. 
Решение лучше и удобнее оформить в виде таблицы:

Ходы	1	2	3	4	5	6
5 л	5	2	2	-	5	4
3 л	-	3	-	2	2	3

Наполняем из бочки 5-литровый сосуд медом (1 шаг). Из 5-литрового сосуда отливаем 3 л в 3-литровый сосуд (2 шаг). Теперь в 5-литровом сосуде осталось 2 литра меда. Выливаем из 3-литрового сосуда мед назад в бочку (3 шаг). Теперь из 5-литрового сосуда выливаем те 2 литра меда в 3-литровый сосуд (4 шаг). Наполняем из бочки 5-литровый сосуд медом (5 шаг). И из 5-литрового сосуда дополняем медом 3-литровый сосуд. Получаем 4 литра меда в 5-литровом сосуде (6 шаг). Задача решена. 
Поиск решения можно было начать с такого действия: к трем литрам добавить 1 литр. Но тогда решение будет выглядеть следующим образом:

Ходы	1	2	3	4	5	6	7	8
5 л	-	3	3	5	-	1	1	4
3 л	3	-	3	1	1	-	3	-

Задача 12

 Бидон емкостью 10 л наполнен парным молоком. Требуется перелить из этого бидона 5 л молока в семилитровый бидон, используя при этом трехлитровый бидон.

Решение: 

Будем "шаги" переливаний записывать в виде строки из трех чисел.При этом сосуды размещены слева направо по мере убывания их вместимости:

Шаги	Бидон
	10 л	7 л	3 л
1-й	3	7	0
2-й	3	4	3
3-й	6	4	0
4-й	6	1	3
5-й	9	1	0
6-й	9	0	1
7-й	2	7	1
8-й	2	5	3

Приложение №2

Логические задачи

Задача 1

Детям 15, 8, 5, 13 лет. Их имена Ваня, Оля, Витя, Гена. Сколько лет каждому из них, если один мальчик ходит в детский сад, Ваня старше Оли, если сложить возраст Вани и Вити, число будет делиться на 3.

Решение:

В детский сад ходит Витя ему 5 лет

Ване 13 лет 13 + 5 = 18(делится на 3)

Оле – 8 (Ваня старше Оли)

Гене – 15 лет

Задача 2

На олимпиаде три команды набрали 285 баллов. При условии, что команда 24-ой школы набрала бы меньше на 8 баллов, 46-ой школы на 12 балов меньше, а команда школы номер 12 на 7 балов меньше, тогда все команды набрали бы баллов поровну. Назови количество баллов, которое набрали команды 12 и 24 школ вместе.

Решение:

1) 12 + 8 + 7 = 27

2) 285 – 27 = 258

3) 258 : 3 = 86

4) 86 + 8 = 94

5) 86 + 12 = 98

6) 86 + 7 = 93

7) 94 + 93 = 187

Задача 3

Лучник сделал 10 выстрелов по мишени, которыми выбил 90 очков. Попаданий в 10 было 4, все остальные выстрелы попадали в семерку, восьмерку или девятку. Сколько было попаданий в каждую цифру кроме десяток.

Решение:

1) 10 * 4 = 40

2) 90 - 40 = 50

3) 10 - 4 = 6

4) 6 * 7 = 42

5) 50 – 42 = 8

6) 8 -1 – 1 = 6

7) 6 : 2 = 3

8) 3 – выстрела по 9, 2 по 8 и 1 по 7.

Задача 4

В банк привезли 1 миллион рублей рублевыми купюрами. Сколько понадобится рабочих дней, чтобы пересчитать купюры, если:

1) Рабочий день 8 часов.

2) Скорость счета 1 купюра в секунду.

3) Счет в рабочий день идет непрерывно.

1 000 000 : 3600 = 41550 рабочих дней 46 минут 40 секунд

Задача 5

В коробке лежат 24 геометрические фигуры (круги, треугольники, квадраты). Известно, что квадратов в 7 раз меньше, чем треугольников. Сколько в коробке лежит каждой из фигур?

Решение:

1) 24: 7 = 3 остаток 3 (3 квадрата не может быть т. к. не остается места для кругов, значит квадратов 2 или 1)

2) Если квадратов 2, то 7 * 2 = 14 (треугольников)

3) 24 – 14 = 10 (кругов и квадратов)

4) 10 - 2 = 8 (кругов)

5) Если квадрат 1 то 7 * 1 = 7 (треугольников)

6) 24 – 7 = 17 (кругов и квадратов)

7) 17 – 1 = 16 (кругов)

Задача 6

Пильщики распиливают бревно на метровые бруски. Длина бревна 5 м. Распиловка бревна поперёк занимает полторы минуты. Сколько минут понадобилось, чтобы распилить бревно?

Решение:

1) 1 мин. 30 сек * 4 = 6 мин.

Задача 7

Масса банки с керосином составляет 350 г, такая же банка меда весит 500 г. Вычисли вес пустой банки, если керосин легче меда в 2 раза.

Решение:

X – керосин

2x - мед

y - банка

X + y = 350 масса банки с керосином

X = 350 – y

2x = 2(350 – y)

2x + y = 500 масса банки с медом

2x = 500 – y

2(350 – y) = 500 – y

700 – 2y = 500 – y

2y – y = 700 – 500

2y – y = 200

y = 200

Ответ: масса пустой банки 200 грамм.

Задача 8

Сколько четырёхместных лодок понадобится, чтобы перевезти одновременно 18 человек?

Решение:

1) 18 : 4 = 4 ост 2

Ответ понадобится 5 лодок. 4 по 4 человека и одна 2 человека.

Задача 9

На двух крышах сидели 16 голубей. После того как с первой на вторую крышу перелетели 5 голубей, а со второй на первую 2 голубя, на обеих крышах голубей стало поровну. Сколько голубей на каждой крыше было сначала?

Решение:

1) 16 : 2 = 8

2) 8 - 2 = 6

3) 6 + 5 = 11

4) 16 - 11 = 5

Ответ: на первой было 11 на вторй 5.

Задача 10

Ваня и Саша подсчитывали, сколько дней в четырёх годах, следующих друг за другом. У Вани получилось 1460 дней, а у Саши - 1461 день. Кто из мальчиков посчитал неправильно?

Решение:

Известно, что раз в четыре года бывает високосный год, в котором 366 дней. Ваня не посчитал его. Поэтому у него вышло неправильно.

Задача 11

Нужно переправить с одного берега на другой козла, капусту и волка. Волка нельзя оставлять с козлом, козла с капустой. В лодке 2 места, то есть с собой можно взять только одного волка, или козла, или одну капусту.

Решение:

Сначала везем козла, возвращаемся, везем капусту на берег где козел, козла забираем обратно на берег где остался волк, волка забираем, козла оставляем, волка отвозим к капусте и возвращаемся за козлом, перевозим козла.

Задача 12

Пятеро каменщиков вначале рабочей недели получили равное количество кирпича. Когда трое из них израсходовали по 326 кирпичей, то у них осталось столько кирпичей, сколько вначале получили другие два каменщика. Сколько всего кирпичей получили каменщики вначале недели?

Решение

По условию задачи каменщиков 5, значит частей тоже 5. Три части из пяти у каменщиков, которые израсходовали по 326 кирпичей, остальные две части у двух других каменщиков. Разница между этими частями одна пятая, которая равна:

326 * 3 = 978(кирпичей);

далее вычисляем, сколько всего было кирпичей:

978 * 5 = 4890.

Ответ: вначале недели каменщики получили всего 4890 кирпичей.

Задача 13

Токарь и его ученик вместе за смену выточили 130 деталей. Сколько деталей выточил каждый из них, если часть деталей, которую выточил токарь, уменьшенная в 3 раза, была равна деталям, которые выточил ученик, увеличенным в 4 раза?

Решение

Пусть ученик выточил x деталей. Тогда:

4x = (130 – x) : 3

130 – x = 4x * 3 = 12x

13x = 130

x = 130 : 13

x = 10 (деталей выточил ученик);

130 – 10 = 120 (деталей) выточил токарь.

Ответ: токарь выточил 120 деталей, ученик 10.

Задача 14

Из автобуса на остановке вышло 6 пассажиров, а вошло 11. На следующей остановке вышло 8, вошло 9. Сколько пассажиров стало в автобусе, если вначале в автобусе было 24 пассажира?

Решение

1) 24 – 6 + 11 = 29 (пассажиров) стало в автобусе после первой остановки;

2) 29 - 8 + 9 = 30 (пассажиров).

Ответ: в автобусе стало 30 пассажиров.

Задача 15

Из двух населенных пунктов, навстречу друг другу одновременно выехали два автомобиля. Первый может преодолеть все расстояние за 6 часов, а второй за 8 часов. Какую часть расстояние они преодолевают за 1 час?

Решение

1) 1/6 + 1/8 = 8/48 + 6/48 = 14/48 = 7/24.

Ответ: за 1 час автомобили приближаются к друг другу на 7/24 всего пути.

Задача 16

От веревки длинной 48 метров отрезали 3/4 части. Какой длины стала веревка?

Решение

1) 48 : 3/4 = 36 (м) отрезали от веревки;

2) 48 – 36 = 12 (м).

Ответ: веревка стала равна 12 метров.

Задача 17

В железнодорожной кассе стоимость билетов для двух детей и трех взрослых составила 900 рублей. Сколько стоит билет для одного ребенка, если взрослый билет стоит 200 рублей?

Решение

1) 200 * 3 = 600 (р.) общая стоимость взрослых билетов;

2) 900 – 600 = 300 (р.) общая стоимость детских билетов;

3) 300 : 2 = 150 (р.)

Ответ: один детский билет стоит 150 рублей.

Задача 18

Велосипедист каждый день преодолевал по 45 км. Сколько километров в день нужно преодолевать велосипедисту, чтобы вернуться обратно за 9 дней, если все путешествие у него заняло 10 дней?

Решение

1) 45 + 10 = 450 (км) всего преодолел велосипедист;

2) 450 : 9 = 50 (км).

Ответ: велосипедисту нужно преодолевать по 50 км в день.

Задача 19

Папе 42 года, он на 29 лет моложе дедушки и в 3 раза старше сына. Сколько лет дедушке и сколько лет сыну?

Решение

1) 42 + 29 = 71 (год) дедушке;

2) 42 : 3 = 14 (лет) сыну.

Ответ: сыну 14 лет, дедушке 71 год.

Задача 20

В городе N статистика показала, что ежегодно количество автомобилей увеличивается на 20%. Во сколько раз увеличится количество автомобилей через 5 лет, если его рост будет продолжаться прежними темпами?

Решение

Увеличение на 20% можно выразить как количество автомобилей умноженное на 1,2.

Следовательно, за 5 лет это количество увеличится на 1,25, что приблизительно равно в два с половиной раза.

Ответ: через пять лет количество автомобилей в городе увеличится приблизительно в 2,5 раза.

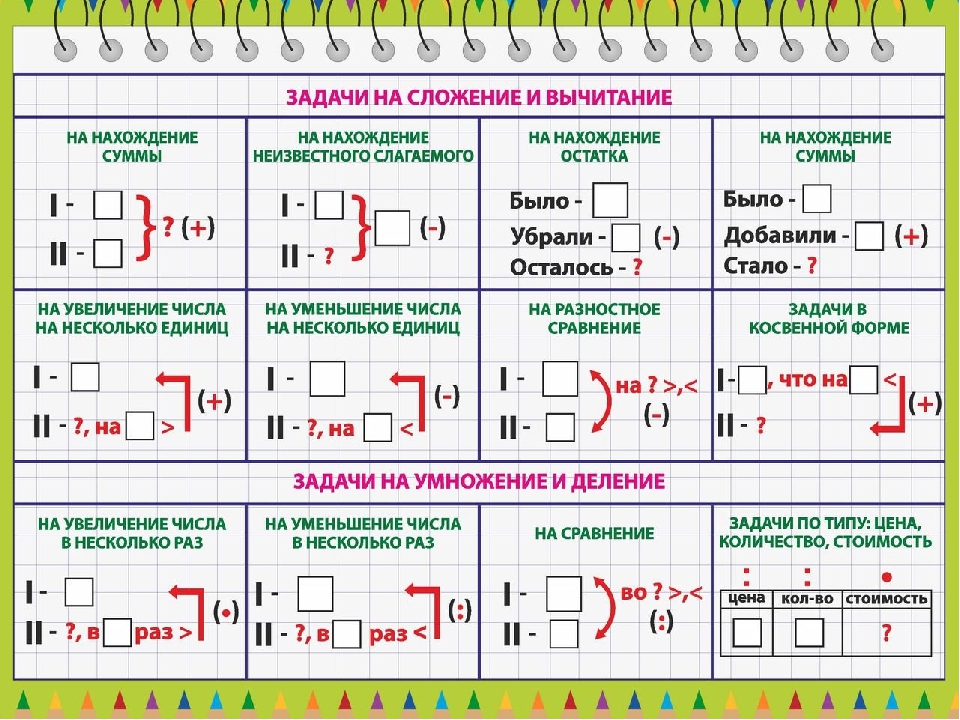
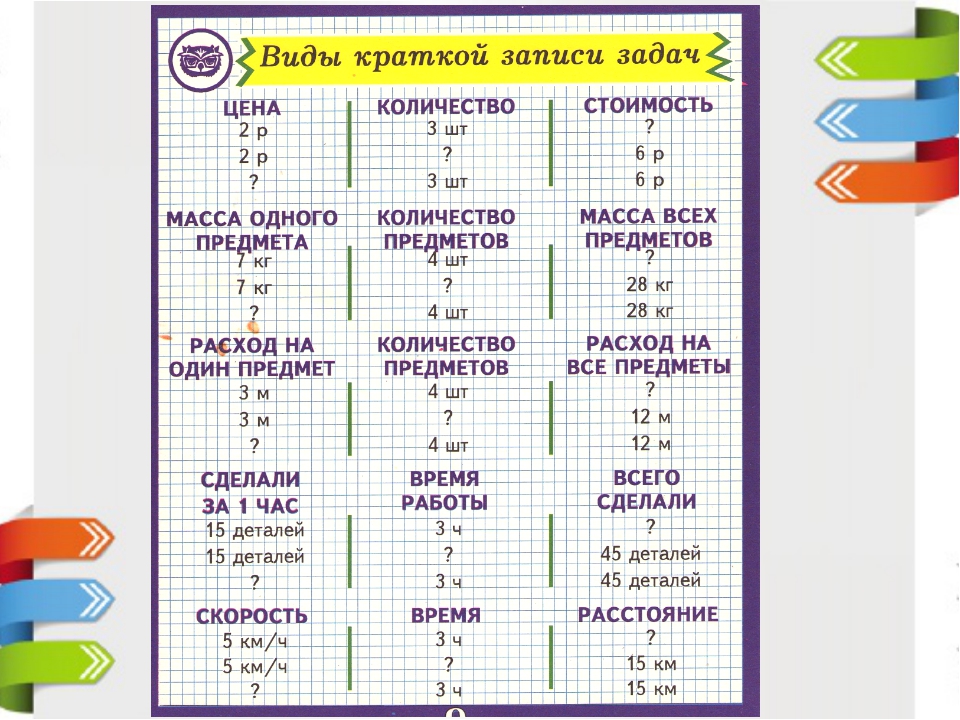
Приложение № 3

«Возможные варианты шпаргалок»