Технологическая карта урока "Решение неполных квадратных уравнений"
|
Предмет |
Алгебра |
|
Класс |
8 |
|
Учитель |
Анисимова Инна Владимировна |
|
Дата |
03.01.2020г |
|
Продолжительность урока |
40 минут |
|
Тема урока |
«Решение неполных квадратных уравнений» |
|
Учебник |
«Алгебра» 8 класс под ред. А.Г. Мерзляк., В.Б. Полонский., М.С. Якир; «Вентана-Граф», 2015 г. |
|
Тип урока |
Открытие новых знаний (конструирование способов действия по ФГОС) |
|
Цель урока |
Организация деятельности учащихся по усвоению понятий квадратного уравнения, неполного квадратного уравнения, способов решения неполных квадратных уравнений. |
|
Задачи по содержанию |
образовательные: создать условия для активной познавательной деятельности учащихся по приобретению новых знаний и расширению понятийной базы за счет включения в нее новых элементов, таких как квадратные уравнения и неполные квадратные уравнения; обеспечить усвоение способов решения неполных квадратных уравнений; развивающие: формировать умения классифицировать уравнения и решать неполные квадратные уравнения; стимулировать познавательную деятельность учащихся; развивать интерес к предмету, четко формулировать свои мысли, применять свои знания на практике; воспитательные: воспитывать умение работать коллективно и самостоятельно (в зависимости от задания), воспитывать дисциплинированность, формирование у учащихся навыков самооценки. |
|
Формы организация учебной деятельности |
Индивидуальная, парная, групповая. |
|
Методы обучения и познания |
Словесные (фронтальная беседа, диалог), иллюстративно-словесный (работа с ЭОР), практический (поиск информации), дедуктивный (анализ, применения знаний, обобщение) |
|
Планируемые результаты изучения темы (требования к уровню подготовки) |
Предметные умения Распознавать квадратные уравнения, классифицировать их. Решать квадратные уравнения-полные и неполные. Проводить простейшие исследования квадратных уравнений. Решать уравнения сводящиеся к квадратным, путем преобразований, а также с помощью замены переменной. Применять теорему Виета для решения разнообразных задач. Решать текстовые задачи алгебраическим способом: переходить от словесной формулировки условия задачи к алгебраической модели путем составления уравнения; решать составленное уравнение; интерпретировать результат. Распознавать квадратный трехчлен, выяснять возможность разложения на множители, представлять квадратный трехчлен в виде произведения линейных множителей. Применять различные приемы самоконтроля при выполнении преобразований. Проводить исследования квадратных уравнений с буквенным коэффициентами, выявлять закономерности. Универсальные учебные действия Л: умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределение функций и ролей участников, взаимодействие и общие способы работы; Р: планирование и прогнозирование своей деятельности, самоконтроль; К: умение владеть приёмами монологической и диалогической речи, работать индивидуально и в группе, формулировать, аргументировать и отстаивать своё мнение; |
|
|
|
|
|
|
Содержание этапов урока
|
Этап урока, цели и задачи |
Время, мин |
Деятельность учителя |
Деятельность учеников |
Задания для учащихся, выполнение которых приведет к достижению планируемых результатов |
|
1.Организационный момент (проверка готовности обучающихся их эмоционального настроя на работу, включение в деятельность на личностно значимом уровне ) Итог: настрой на работу |
1 мин. |
Обеспечивает благоприятный настрой. -Здравствуйте, ребята! Математику не зря называют «Царицей наук». Одно из замечательных свойств математики – любознательность. Давайте постараемся сегодня проявить свою любознательность на уроке. |
-приветствие учителя; -полная готовность к уроку; -настрой на работу; -организация внимания; -оценивают готовность к уроку. |
|
|
2. Актуализация опорных знаний урока. Проверка опорных знаний учащихся, необходимых для изучения нового материала. Выявление типичных ошибок и пробелов в ЗУН для дальнейшей коррекционной работы Итог: определение степени усвоения учащимися материала |
5 мин |
Создать ситуацию, успеха, путем проверки владения материала прошлых уроков. Организует работу по актуализации опорных знаний. |
Устное решение или краткая запись решения выражений |
1. Представить выражение в виде одночлена: а)
2. Вычислить: а)
3. Решить уравнения : а)
в)
|
|
3. Постановка проблемы. Определение совместной цели деятельности |
3 мин. |
Создает проблемную ситуацию, объясняет учебную задачу, наблюдает, консультирует. |
Отвечают на вопросы, формулируют цель урока |
Впервые
квадратное уравнение сумели решить
математики Древнего Египта. В одном
из математических папирусов содержится
задача: «Найти стороны поля, имеющего
форму прямоугольника, если его площадь
12, а
Пусть
х- длина поля. Тогда
12 Итак,
Задачи на квадратные уравнения встречаются уже в 449 году. В древней Индии были распространены публичные соревнования в решении трудных задач. Часто они были составлены в стихотворной форме. Вот одна из задач знаменитого индийского математика XII века Бхаскары звучит так Обезьянок резвых стая, Власть поевши, развлекалась. Их в квадрате часть восьмая На поляне забавлялась, А двенадцать по лианам Стали прыгать, повисая… Сколько ж было обезьянок, Ты скажи мне в этой стае? Решение:
После рассмотрения данных задач, не решая их (учащиеся пока не умеют этого делать), учащиеся пытаются сформулировать тему и цель урока. Открыли тетради, записали тему урока. |
|
4. Изучение нового материала (усвоение новых знаний и умений и способов действий) с первичным закреплением знаний, проверкой применения знаний и умений в новой ситуации. |
15 мин |
Организует усвоение нового знания. Организует работу по выполнению упражнений с проговариванием во внешней речи. Осуществляет контроль за процессом решения задач. |
Отвечают на вопросы, учатся классифицировать уравнения, записывают алгоритм решения уравнений в тетрадь |
Мы с вами начали изучать большой раздел «Квадратные уравнения».
Коэффициенты а, в, с называют так: а –первый коэффициент, в – второй коэффициент, с – свободный член. Примеры квадратных уравнений №512 стр.114 учебника.
Пример
1
(из египетской задачи)
По
смыслу задачи принимаем во внимание
только
если Здесь можно сделать вывод (вместе с учащимися): если коэффициенты а и с имеют разные знаки, то уравнение имеет 2 корня, если же коэффициенты а и с имеют одинаковые знаки, то уравнение корней не имеет. Пример
2.
х(4х + 9) = 0 х = 0 или 4х = -9 х
= -2
х(ах + в)=0 х = 0 или ах +в =о ах= -в х
=-в/а Уравнения вида
Пример
3.
|
|
5. Физкультминутка ПРОВЕСТИ ПО ХОДУ УРОКА! |
1 мин. |
Сменить деятельность, обеспечить эмоциональную разгрузку учащихся. Показ упражнений. |
Учащиеся сменили вид деятельности и готовы продолжить работу |
Учитель показывает на доске уравнения и дети приседают, если уравнение неполное и встают, если это полное квадратное уравнение. |
|
6. Закрепление нового материала. Итог: Определение степени усвоения полученных знаний |
10 мин. |
Организует самостоятельную работу по закреплению изученного с последующей проверкой. Выявляет качество и уровень усвоения знаний, а также устанавливает причины выявленных ошибок. Организует работу в парах. Контролирует деятельность учащихся, при необходимости консультирует в появившихся вопросах. |
Выполняют задание. Работа в парах. |
Выполняем задания из учебника Парная работа. № 616 и № 617 В предложенных вариантах ОГЭ 9 класса найти задания с неполными квадратными уравнениями.(На экране) -Знания, полученные на уроках математики вам необходимы при сдачи ОГЭ в 9 классе. |
|
7. Рефлексия |
3 мин. |
Инициировать рефлексию детей по их собственной деятельности и взаимодействия с учителем и другими детьми в классе. |
Отвечают на вопросы, рассказывают, что узнали, смогли выполнить. Оценивают свою учебную деятельность |
Что вы нового узнали на уроке? Чему вы научились на уроке? - Оцените свою деятельность на уроке и настроение, используя один из трех кружочков, смайликов лежащих на парте, прикрепить к доске: -Я все понял и мне было интересно -Я понял на уроке, но у меня есть вопросы -Я ничего не понял на уроке, мне было скучно |
|
8. Домашнее задание |
2 мин. |
Обеспечение понимания детьми цели, содержания и способов выполнения домашнего задания |
Открывают дневники, записывают домашнее задание, задают вопросы. |
№ 618, №619 Поясняет выполнение номеров. |
- Международный вебинар «Обучение грамоте старших дошкольников с помощью развивающих игр В. В. Воскобовича: практика реализации ФГОС и ФОП ДО»
- Вебинар «Социализация и социальные навыки дошкольников: учимся общаться, договариваться, взаимодействовать»
- Вебинар «Нейропсихологические методы диагностики и коррекции нарушений в развитии гиперактивных детей»
- Международный вебинар «Общие и специфические образовательные потребности обучающихся с нарушениями слуха и способы их реализации»
- Международный вебинар «Волонтёрство и новые воспитательные практики в школе»
- Вебинар «Библиотечный бренд»






 ; б)
; б)
 ;
; ; б)
; б)
 ;
; ; б)
; б)
 ;
; ; г)
; г)
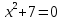 .
. длины равны ширине».
Рассмотрим её
длины равны ширине».
Рассмотрим её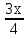 – его ширина,
– его ширина,  – площадь. Получилось квадратное
уравнение:
– площадь. Получилось квадратное
уравнение:
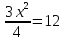 .
В папирусе дано правило для его решения:
«Раздели 12 на
.
В папирусе дано правило для его решения:
«Раздели 12 на = 16.
= 16.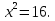 «Длина
поля равна 4» - сказано в папирусе.
Прошли тысячелетия, в алгебру вошли
отрицательные числа. Решая уравнение
«Длина
поля равна 4» - сказано в папирусе.
Прошли тысячелетия, в алгебру вошли
отрицательные числа. Решая уравнение
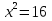 ,
мы получаем два корня
,
мы получаем два корня
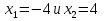 .
Разумеется, в египетской задаче и мы
приняли бы х = 4, т.к. длина поля не может
быть отрицательным числом.
.
Разумеется, в египетской задаче и мы
приняли бы х = 4, т.к. длина поля не может
быть отрицательным числом.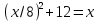
 – 64 + 768 = 0
– 64 + 768 = 0 (решение
данной задачи рассмотреть на следующих
уроках)
(решение
данной задачи рассмотреть на следующих
уроках)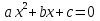 ,
где х – переменная; а, в, с – некоторые
числа, причем а
,
где х – переменная; а, в, с – некоторые
числа, причем а
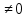 .
. называют неполным, если хотя бы один
из коэффициентов а, в или с, равен
нулю. Примеры в№512 д),е).
называют неполным, если хотя бы один
из коэффициентов а, в или с, равен
нулю. Примеры в№512 д),е).
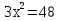

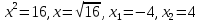

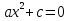

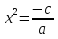 ; если
; если
 ,
то уравнение имеет два корня;
,
то уравнение имеет два корня; ,
то уравнение не имеет корней.
,
то уравнение не имеет корней.
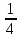

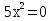 ,
х = 0
,
х = 0 ,
х
= 0 – единственный корень
,
х
= 0 – единственный корень