Развитие вычислительных умений и навыков

Выполнил: учитель математики

МБУ СОШ №70

Эрбис А.С.

г. Тольятти, 2015 г.

Формирование вычислительных умений и навыков традиционно считается одной из самых «трудоемких» тем. Вопрос о значимости формирования устных и письменных вычислительных навыков на сегодняшний день является весьма значимым в методическом плане. Широкое распространение калькуляторов ведет за собой необходимость уделять большее внимание отработки этих навыков. Однако внимание к устным арифметическим вычислениям является традиционным для образовательной школы. Именно поэтому необходимо часто пользоваться математическими приемами и операциями на уроках, чтобы сформировать вычислительные навыки – устные и письменные.

Умение выполнять вычисления быстро и пользоваться приемами, упрощающие математические действия, как раз и будет означать формирование вычислительного навыка. Что такое навык? Но перед тем как ответить на этот вопрос необходимо знать, что означают понятия «умения» и «знания». В педагогическом словаре Коджаспировой Г.М и Коджаспирова А.Ю [3] даются такие определения:

Умение — подготовленность к практическим и теоретиче­ским действиям, выполняемым быстро, точно, сознательно, на основе усвоенных знаний и жизненного опыта У. формируется пу­тем упражнений и создает возможность выполнения действия не только в привычных, но и в изменившихся условиях. 

Знание (в широком смысле слова) — проверенный практи­кой результат познания действительности, верное ее отражение в мышлении человека; выступает в виде понятий, законов, прин­ципов, суждений, бывает эмпирическим, выведенным из опыта, практики, и теоретическим, отражающим закономерные связи и отношения; (в пед.) — понимание, сохранение в памяти и вос­произведение фактов науки, понятий, правил, законов, теорий. Усвоенные знания отличаются полнотой, системностью, осознан­ностью и действенностью.

Навык — действие, доведенное до автоматизма; формирует­ся путем многократного повторения. В процессе обучения необхо­димо вырабатывать навыки, особенно общеучебные, межпредмет­ного значения: письменной и устной речи, решения задач, счета, измерений и т. п.

Что в педагогике имеется в виду под «вычислительные навыки»? Вычислительный навык – это высокая степень овладения вычислительными приемами.

Приобрести вычислительные навыки – значит, знать для каждого случая, какие операции, действия необходимо выполнять в определенном порядке, чтобы найти результат, и выполнить эти операции без больших затрат времени.

Вместе с тем, ученик при выполнении вычислительного приема должен отдавать отчет в правильности и целесообразности каждого выполненного действия, то есть постоянно контролировать себя, соотнося выполняемые операции с образцом – системой операций. О сформированности любого умственного действия можно говорить лишь тогда, когда ученик сам, без вмешательства со стороны, выполняет все операции приводящие к решению. Умение осознано контролировать выполняемые операции позволяет формировать вычислительные навыки более высокого уровня, чем без наличия этого умения.

В начале 1930-х гг. Леонтьев А.Н. встал во главе харьковской деятельностной школы и приступил к теоретической и экспериментальной разработке проблемы деятельности. В результате им была выдвинута концепция деятельности, являющаяся в настоящее время одним из признанных теоретических направлений современной психологии.

Основными понятиями в этой теории являются деятельность, сознание и личность.

Деятельность человека имеет сложное иерархическое строение. Она состоит из нескольких неравновесных уровней. Верхний уровень – это уровень особых видов деятельности, затем следует уровень действий, за ним – уровень операций, и самый низкий – уровень, психофизических функций.

Выготский Л. С.  считает, что проблема умствен­ного развития учащихся в процессе обучения есть «самый цент­ральный и основной вопрос» в психолого-педагогической науке. Его успешное развитие зависит от того, каким образом будет проходить обучение в школе. А это в свою очередь, теснейшим образом связано с развитием школы и системы образования.

Выготский Л. С. говорит, что «для динамики умственного раз­вития в школе и для относительной успешности ученика более важен, более влиятелен, более могуществен не уровень умствен­ного развития на сегодняшний день, который является не боль­ше чем предпосылкой, но функции, находящиеся в стадии созре­вания. То, что созревает, оказывается более важным».

Теория поэтапного формирования умственных действий -(разработана П.Я.Гальпериным и его сотрудниками) - учение о процессах и условиях, определяющих формирование осмысленных действий, а на их основе - представлений и понятий об их объектах.

Процесс формирования умственных действий совершается поэтапно:

1. Выявление ориентировочной основы действия. На этом этапе происходит ориентация в задании первоначально выделяется то, что само бросается в глаза.

2. Происходит формирование действия в материальном виде. На этом этапе обучающийся умственным действиям получает полную систему указаний и систему внешних признаков, на которые ему надо ориентироваться. Действие автоматизируется, делается целесообразным, возможен его перенос на аналогичные задания.

3. Этап внешней речи. Здесь действие подвергается дальнейшему обобщению благодаря его полной вербализации в устной или письменной речи. Таким образом, действие усваивается в форме, оторванной от конкретики, т.е. обобщенной. Важное значение приобретает не только знание условий, но и понимание их.

4. Этап формирования действий во внешней речи про себя. Этап внутренней деятельности. Так же как и на предыдущем этапе, действие проявляется в обобщенном виде, однако его вербальное освоение происходит без участия внешней речи. После получения мыслительной формы действие начинает быстро редуцироваться, приобретая форму идентичную образцу, и подвергаясь автоматизации

5. Формирование действий во внутренней речи. Этап интериоризации действия. Действие становится здесь внутренним процессом, максимально автоматизированным, становится актом мысли, ход которого закрыт, а известен только конечный "продукт" этого процесса. [5]

Применение вычислительных навыков сопровождается в примерах задач, в которых решение сводится к громоздким арифметическим действиям, которые зачастую встречаются в Государственной Итоговой Аттестации и в Едином Государственном Экзамене. Одним их таких примеров является работа с квадратным корнем.

Например. Найти чему равно , если a=4; b=; c=7; .

Решение.

Для начала найдем чему равно p. . Подставим a, b, c и p d R.

.

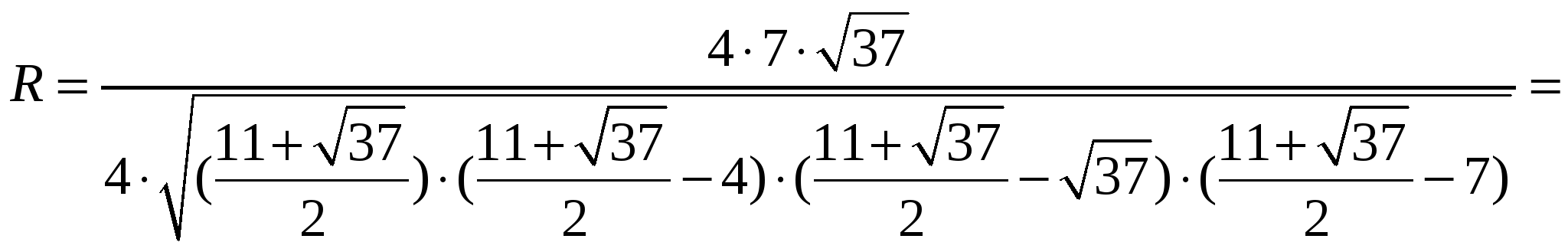
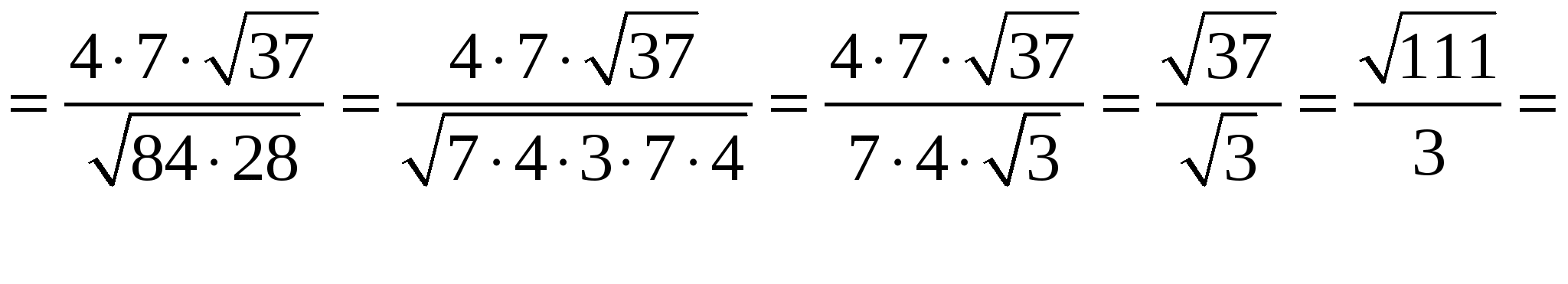
Вынесем в знаменателе из под корня и запишем 4 в числитель. Получаем:

.

Выполняя это задание на итоговой аттестации, использование калькулятора недопустимо. Поэтому требуется владение специальными приемами быстрого счета или, говоря обобщено, вычислительными навыками. Некоторыми необходимо пользоваться устно, а другими письменно.

Приемов быстрого счёта существует огромное множество. Например: прием, основанный на знании законов и свойств арифметических действий; прием округления; прием перестановки слагаемых или перестановки сомножителей; прием замены одного действия другим; прием умножения на …

Все эти приемы можно объединить в две группы:

- общие (приемы, в которых используются свойства арифметических действий, используются для любых чисел)

- специальные (для конкретных чисел, частные случаи).

В процессе познавательной деятельности целесообразно осваивать как общие, так и специальные приемы быстрого счета. Но особое внимание стоит уделять принципам умножения на …

Методические приемы освоения вычислительных навыков основаны на признаках делимости. Как правило, признак делимости основан на действиях с частью цифр из записи числа. Признаки делимости на 2, 3, 5, 9, 10 даются школьникам на уроках математики в 5 классе.

Например. Число 13 483 не делится на 2, а число 137 836 делится на 2, т.к. последняя цифра числа 137 836 делится на 2, то есть является чётной.

Помимо этих признаков, полезно знать еще признаки делимости на 4, 6, 7, 8, 11, 12, 13, 14, 15, 17, 19, 23, 25, 99, 101. Они существенно ускоряют процесс выполнения заданий не только на ГИА, но и на ЕГЭ.

Очевидно, что вычислительные навыки является необходимыми элементами общеобразовательной подготовки учащихся, прежде всего силу своей практической значимости. Начиная с таблицы умножения в начальных классах, сущность которой основана на способе сложения, продолжая работой со степенями, которая в полной мере построена на умножении чисел. Зная приемы быстрых вычислений и признаков делимости, можно существенно ускорить процесс выполнения тех или иных примеров, правильность которых, в большой степени зависит от быстрых и верных вычислений.

Таким образом, без вычислений не обойтись как в повседневной жизни, так и во время учебы в школе. Поэтому знание простейших правил вычислений позволяет ускорить процесс обучению математики.

Список использованной литературы

1. Будлянская Н. Л. Сумина Г. Н. Решение текстовых задач: Пособие для учащихся. – Комсомольск-на-Амуре: Издательство Комсомольского-на-Амуре государственного педагогического университета, 2004. – 54 с.

2. Груденов, Я.И. Совершенствование методики работы учителя математики – М.: Просвещение, 1990. – 224 с.

3. Коджаспирова, Г.М. Педагогический словарь для студентов высш. и ср. пед. учеб. заведений / Г.М. Коджаспирова, А.Ю. Коджаспиров. - М.: Академия, 2000. - 175 с.

4. Саранцев, Г.И. Методика обучения математике в средней школе: учеб. пособие для студентов мат. спец. пед. вузов и ун–тов / Г.И. Саранцев. – М.: Просвещение, 2002. – 224 с.

5. http://www.hr-portal.ru/article/kontseptsiya-poetapnogo-formirovaniya-umstvennykh-deistvii-pyagalperina