Бюджетное общеобразовательное учреждение Нюксенского муниципального района Вологодской области «Левашская основная общеобразовательная школа»,

Принято Утверждаю:

на заседании педагогического совета школы Директор школы

Протокол № 1 от 27.08.2019 г. Попова Г.А.

Приказ № ________ от ____.08.2019 г.

Рабочая программа внеурочной деятельности

по общекультурному направлению

«Математика и фольклор»

для обучающихся 5-6 классов

Составитель:

Чадромцева В.Г., учитель математики

БОУ Ню Мр ВО «Левашская ООШ»

2019-2020 учебный год

Пояснительная записка

Народное творчество зародилось в глубокой древности. Фольклор возник еще в те времена, когда не было письменности, поэтому произведения передавались от человека к человеку, из уст в уста. В этом главное отличие фольклора от литературы, устного искусства слова от письменного.

Слово «фольклор» впервые употребил в одной из своих статей английский историк Вильям Томсон в 1846 году. В переводе с английского «фольклор» означает «народная мудрость». «Американские и западноевропейские ученые фольклором называют все виды народного искусства – музыку и танцы, резьбу по дереву и вышивку, словесное творчество. А российские ученые словом фольклор обозначают лишь словесное искусство народа» [7, с. 402-403].

Произведения устного народного творчества складывались на протяжении многих столетий. В «Словаре литературных терминов», составленном И.В. Клюхиной, предлагается такое определение: «устное народное творчество – художественная творческая деятельность народа, отражающая его жизнь, воззрения, идеалы» [5, с. 81]. Таким образом, термины «фольклор» и «устное народное творчество» в русском языке являются синонимами. Обратимся к жанрам русского устного народного творчества. Термин «жанр» заимствован из французского языка и в переводе означает «род, вид». В общем смысле жанр – это «сочетание отличительных особенностей произведения» [5, с. 18], а фольклорный жанр – это «род произведений устного народного творчества» [5, с. 83].

Фольклорными жанрами являются: песня, сказка, былина, баллада, легенда, предание, пословица, поговорка, скороговорка, закличка, потешка, пестушка, прибаутка, небылица. Составители «Словаря литературных терминов» относят потешки, пестушки, прибаутки и небылицы к детскому фольклору. Составители энциклопедии по литературе «Я познаю мир» фольклорными также называют такие жанры, как частушка, загадка, считалка и дразнилка.

Былина – жанр, характерный только для русского фольклора. Это «песня-сказание о богатырях и исторических событиях Древней Руси» [5, с. 12]. Место и время в былине называются точно, а события вымышлены. Известные былины: «Садко», «Илья Муромец», «Илья Муромец и Соловей-разбойник», «Добрыня и Змей».

Сказка – это жанр фольклора, который имеет три признака: устность, коллективность и анонимность. Фольклорные сказки бывают трех видов: сказки о животных, волшебные и социально-бытовые. В сказках о животных главными персонажами являются животные, которым иногда противостоит человек (например, сказка «Кот, петух и лиса»). В волшебных сказках действуют люди и фантастические существа, это «история о том, как главный герой сталкивается с бедой или трудностями и как он их преодолевает» [5, с. 69]. Примером волшебной сказки является «Сказка о молодильных яблоках и живой воде». В социально-бытовых сказках герои становятся победителями не благодаря волшебству, им помогает собственный ум, смекалка, хитрость (например, сказка «Каша из топора»).

Следующий широко известный фольклорный жанр – это загадки. Загадка – это «иносказательное поэтическое описание какого-либо предмета или явления, испытывающее сообразительность отгадывающего» [5, с. 19]. Загадка представляет собой логическую задачу. Чтобы ее отгадать, нужно найти ответ на вопрос. В загадках есть рифма, слова созвучны друг другу. Вот такая есть русская народная загадка о солнце: «Что выше леса, краше света, без огня горит?»

Наконец, обратимся к такому жанру, как скороговорка. В словаре С.И. Ожегова дается следующее толкование: «скороговорка – это искусственно, ради забавы придуманная фраза с труднопроизносимым подбором звуков, которую нужно произнести быстро, не запинаясь» [4, с. 629]. Одна из самых известных русских скороговорок: «На дворе – трава, на траве – дрова».

Таким образом, русский фольклор интересен современному читателю тем, что он позволяет узнать историю, быт, особенности характера наших предков. В фольклорных произведениях народ отражал свои представления об устройстве мира, об обществе и других людях. Устное народное творчество – это настоящий кладезь знаний. Из приведенного перечня фольклорных жанров в дальнейшей работе мы будем использовать былинные и сказочные сюжеты, а также загадки и скороговорки.

Данная тема является актуальной, так как отражает межпредметные связи. В современном мире тот человек становится успешным, кто умеет применять и объединять в своей работе знания из различных областей.

В связи с этим был выбран объект исследования – русское устное народное творчество. Предмет исследования – элементы русского фольклора при изучении математики в 5 и 6 классах.

Цель – изучение возможностей использования фольклорного материала на уроках математики в 5 и 6 классах. Для достижения поставленной цели необходимо решить несколько задач.

1. Определить, что такое фольклор и каковы его жанры.

2. Выяснить, применяются ли на уроках математики в 5 и 6 классах задания, включающие фрагменты фольклорных произведений.

3. Провести первичное анкетирование и выявить уровень интереса учащихся к урокам математики.

4. Составить и использовать на уроках математики комплекс заданий с фольклорными элементами.

5. Определить значимость проведенной работы по результатам повторного анкетирования.

Задачи: Знакомство с жанрами русского фольклора. Развитие познавательных интересов, интеллектуальных и творческих способностей. Формирование навыков самостоятельной работы с научно-популярной и художественной литературой. Формирование навыков работы в группе Развитие навыков оформления полученных результатов

Математика и окружающий нас мир очень взаимосвязаны. И эту взаимосвязь можно показать через задачи, связанные с народным фольклором. С помощью фольклора можно увидеть красоту математических закономерностей, которые описывают многие процессы и явления окружающей действительности.

Рассмотрены вопросы фольклора как средства формирования математических представлений. Мною в Интернете были найдены задачи с фольклорным характером работы.

Данная программа внеурочной деятельности школьников составлена на основе:

1. Виленкин Н.Я. Математика. 5 класс: учеб. для учащихся общеобразоват. учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – М.: Мнемозина, 2013. – 280 с.

2. Виленкин Н.Я. Математика. 6 класс: учеб. для учащихся общеобразоват. учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – М.: Мнемозина, 2013. – 280 с.

3. Волина В.В. Пословицы, поговорки, ребусы / Ред. Н.Б. Петрова. – СПб: «Дидактика-плюс», 1997. – 224 с.

4. Золотой клубочек: Русские народные загадки / Сост. Т.А. Климова. – Иркутск: Восточно-Сибирское книжное издательство, 1994. – 128 с.

5. Ожегов С.И. Словарь русского языка: Ок. 57000 слов. – Екатеринбург, «Урал-Советы» («Весть»), 1994. – 800 с.

6. Словарь литературных терминов / Сост. И.В. Клюхина. – 2-е изд., перераб. – М.: ВАКО, 2012. – 96 с.

7. Тридцать три Егорки: Русские народные скороговорки / Сост. Г. Науменко. - М.: Детская литература, 1989. – 32 с.

8. Я познаю мир: Дет. энцикл.: Литература / Авт.-сост. Н.В. Чудакова; Худож. Е.В. Гальдяева, А.В. Кардашук; Под общ. ред. О.Г. Хинн. – М.: ООО «Фирма «Издательство АСТ», 1999. – С. 402-403

Результаты освоения содержания программы

У учащихся могут быть сформированы личностные результаты:

-ответственное отношение к учению, готовность и способность обучающихся к самообразованию на основе мотивации к обучению и познанию,

-осознанный выбор и построение дальнейшей индивидуальной траектории образования на базе ориентировки в мире профессий и профессиональных предпочтений, с учётом устойчивых познавательных интересов;

-способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;

-умение контролировать процесс и результат математической деятельности;

-первоначальные представления о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации;

-коммуникативная компетентность в общении и сотрудничестве со сверстниками в образовательной, учебно-исследовательской, творческой и других видах деятельности;

-критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;

-креативность мышления, инициативы, находчивости, активности при решении задач.

Метапредметные результаты:

регулятивные

учащиеся получат возможность научиться:

-составлять план и последовательность действий;

-определять последовательность промежуточных целей и соответствующих им действий с учётом конечного результата;

-предвидеть возможность получения конкретного результата при решении задач.

познавательные

учащиеся получат возможность научиться:

устанавливать причинно-следственные связи; строить логические рассуждения, умозаключения (индуктивные, дедуктивные и по аналогии) и выводы;

формировать учебную и общекультурную компетентность в области использования информационно-коммуникационных технологий;

видеть математическую задачу в других дисциплинах, окружающей жизни;

выдвигать гипотезу при решении учебных задач и понимать необходимость их проверки;

планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;

выбирать наиболее эффективные и рациональные способы решения задач.

коммуникативные

учащиеся получат возможность научиться:

организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников;

взаимодействовать и находить общие способы работы;

работать в группе; находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов; слушать партнёра; формулировать, аргументировать и отстаивать своё мнение;

прогнозировать возникновение конфликтов при наличии различных точек зрения;

разрешать конфликты на основе учёта интересов и позиций всех участников;

координировать и принимать различные позиции во взаимодействии;

аргументировать свою позицию и координировать её с позициями партнёров в сотрудничестве при выработке общего решения в совместной деятельности.

Тематическое планирование

№п/п	Тема занятия	Количество часов
1.	Историческая справка. Математическая информация в народных сказках. Символические и особые числа в сказках.	1
2	Как математики рассказывают сказки. Математические сказки.	1
3	Задачи из сказок	2
4	Сказочные герои в математических задачах	2
5	Старинные меры счисления в литературе	2
6	Математики – литературы. Литературно-математическая викторина.	1
7	Задачи – один из видов народного творчества	1
8	Геометрические фигуры в рисунках хоровода	1
9	Орнамент в математике	2
10	Загадки и математика	2
11	Математика в скороговорках	1
12	Математические формулы, теоремы и правила в частушках.	1
13	Пословицы и поговорки в графиках и диаграммах	2
14	Дразнилки и считалки с числами. Числа в русских народных пословицах.	1
15	Математический фольклор народов мира	2
16	Военно-патриотические задачи	2
17	Краеведческий фольклор	3
16	Сказки, сочиненные учениками и учителями.	1
17	Проектная деятельность	6

Занятие 1. Историческая справка. Математическая информация в народных сказках. Символические и особые числа в сказках.

Математика – настоящее волшебное царство. А цифры, числа, геометрические фигуры, если вы сильно захотите, могут превратиться в удивительные сказочные персонажи .

Первые математические понятия вы узнаёте из сказок: 1) числа (Белоснежка и семь гномов, Три поросёнка), 2) счёт (Рукавичка), 3) сравнение (Три медведя, Дюймовочка), 4) геометрические фигуры (Колобок ).

Математика ум в порядок приводит,

Математика неизвестное находит,

Математика дарит нам радости чувство,

Математика - это наука – искусство.

Сказки в математике. Звучит необычно и как-то странно.

Со сказками мы привыкли сталкиваться на уроках литературы. Сказки – это приключения, мы несерьезно относимся к ним.

А математика – царица всех наук. С начальной школы нас приучают быть внимательными, трудолюбивыми и серьезными с этой особой. Мы привыкли, что математика – наука сухая и не всегда интересная, говорящая на своем языке формул, уравнений, рассуждений, доказательств, графиков…Но ведь это совсем не значит,  что слова «сказка» и «математика» не могут стоять рядом. Конечно, могут!

Присутствие чисел в сказках наблюдается повсюду и почти всегда они выступают как священные и глубоко символические. Число один встречается в русской традиции крайне редко. Однако образ Аники воина, который выезжает в Чисто Поле, чтобы биться с врагом одному, а также символ копья и единорога, встречающиеся в текстах летописей и древних преданий говорят об обратном. Число два олицетворяет идею чета и нечета, выражает собой соотношения правого и неправого начал. Славянскую сказку пронизывает идея борьбы таких начал как Жизнь и Смерть, живая и мертвая Правда и Кривда. Гораздо чаще в русской сказке и фольклоре говорят о числе семь. Это и семь богов древнерусского пантеона, и бог Семаргл, явно ведущий свое имя от числа 7, и семь небес, и многие другие семеричные символы, разбросанные по многочисленным легендам, сказкам и преданиям. "7 - число человеческое - (семь отверстий в человеческой голове), семь возрастов, семь добродетелей.

Кто из нас не помнит знаменитого сказочного зачина: « За тридевять земель в тридевятом царстве жили-были…» И кто из нас, зачитываясь в детстве сказками. Не сталкивался с таинственным числом « три».

У крестьянина три сына:

Старший умный был детина,

Средний сын - и так и сяк,

Младший вовсе был дурак.

И вот этого младшего, любимого всеми Иванушку-дурочка, судьба всегда трижды испытывает.

А пословицы и поговорки? Ведь буквально пересыпаны числом три: «в трех соснах», «в три ручья», «с три короба».

Так откуда оно взялось это магическое «три»?

Любопытно, что число 3 рассматривали не только как счастливое («бог троицу любит»), но и как несчастливое («треклятый»).

Число 9 находится в непосредственной связи и зависимости от числа три. От 3 х 3= 9 делается шаг к 3 х 9 = 27. Это число тоже имеет магическую силу. От него и идет знаменитое сказочное «за тридевять земель».

1. «В тридевятом царстве, в тридесятом государстве жил-был царь и было у него три сына…»

2. Камень на распутье предлагает богатырю три пути…

3. Отправляют героев сказок за тридевять земель в тридесятое государство

А где это государство? Оказывается рядом…

Решение: 3х9=27дней (27 дней – лунный месяц – время

обращения Луны вокруг Земли)

3х10=30 дней (30 дней - период между двумя

новолуниями)

Ответ: Тридевятое царство, тридесятое государство находится на расстоянии, равному месяцу пути.

С числами, которые называют магическими, сталкивались все. В сказках, легендах, пословицах и поговорках, в календарях и на циферблатах, в ритуалах и культах мы встречаем Святую Троицу, три желания, семь дней недели, семерых козлят, 12 месяцев.

Число «три» встречается во многих пословицах и поговорках: «в трех соснах», «в три ручья», «с три короба» и так далее.

Само наблюдение над природой наводило на мысль об особом значении этого числа. Люди всюду встречали или думали, что встречают, деление на 3. Они видели, что вселенная состоит из неба, земли и воды; перед ними стояли небесные светила - солнце, луна и звезды; в телах они наблюдали три измерения - длину, ширину и высоту; во времени - прошлое, настоящее и будущее. А так как религия древних была связана с явлениями природы, то деление на три они положили в основу своих теоретических систем, и это число получило значение священного. Пифагорейцы считали число 3 совершенным, потому что оно имеет начало, середину и конец, и изображали его в виде треугольника.

Число 3 вошло в христианскую религию, верующие представляют Бога в виде триединства: отец - сын - святой дух. Это число легло в основу композиционного построения ряда художественных произведений.

Любопытно, что число 3 рассматривали не только как счастливое («Бог троицу любит»), но и как несчастливое («треклятый»).

Число 9 находится в непосредственной связи и зависимости от числа 3. Иногда оно мыслится как число 3, только в усиленной форме: 9 = 3x3. Интересно, что если в древнейших преданиях говорится о трех музах, то в более поздних - преимущественно о девяти. Числа 3 и 9 находили особое применение и в бытовых отношениях. Например, на пирах существовало правило - пить 3 чаши или 9, но никогда не 4 или 5. В речи ряда народов символом грозной опасности или наивысшего подъема, могучей силы выступает «девятый вал». Он как бы венчает какой - то процесс и кладет начало переходу к новому качеству.

У славян поминки по усопшему отправляются на 9-й день после его кончины. По - видимому, это тоже свидетельствует о каком - то процессе обновления, но уже в потустороннем мире.

От 3 х 3 = 9 делается шаг к 3 * 9 = 27. Это число тоже имеет магическую силу, например, при заклинании духов болезней. От него происходит и знаменитое сказочное «за тридевять земель».

Число 7 буквально пронизывает всю историю культуры народов Земли.

Зародился культ числа 7 в Древнем Вавилоне. Наблюдая небо, древние астрономы насчитывали 7 планет: Солнце, Луну, Меркурий, Венеру, Марс, Юпитер и Сатурн. Они подметили, что планеты, хоть и запутанно, двигаются по определенной небесной дороге среди определенного круга небесных созвездий.

Пятерка считалась числом небесного, лунного мира; семерка принадлежала миру солнечному, подземному. Первая представлялась счастливым числом, а вторая - несчастливым. Впоследствии, когда Солнце заняло ведущую роль в религии древних, число 7 стало символом благоприятствия.

В Древнем Вавилоне самым замечательным числом было 12. На 12 месяцев, по числу созвездий Зодиака, вавилоняне делили год. Сутки они делили на - 24 или 12 двойных часов, каждый час на 60 минут, или 5 раз по 12. Кроме того, это число было очень удобно для счета: его можно без остатка делить на 2, на 3, на 4 и на 6. Число 12 вошло во многие системы счета. Так, в ряде стран считали дюжинами (дюжина - 12 штук). Английский фут равен 12 дюймам, шиллинг - 12 пенсам. «Удобство» этого числа сказалось и в религиях: у Христа, а до него у Будды, было 12 последователей - учеников.

Совсем непохожим на 12 было число 13. Его нельзя было разделить ни на одно число, кроме него самого и единицы. Поэтому и стали его считать несчастливым, «чертовой дюжиной». Кстати, у древних евреев числа обозначались буквами. Число 13 начиналось с буквы «м», и с этой же буквы начиналось слово «мэм» - смерть. Очевидно, это тоже сыграло свою роль в наделении числа 13 отрицательными качествами.

Долгое время у многих народов, в том числе и у славян, самым большим из известных им чисел было число 40. А все, что лежит за пределами этого числа, - неопределенное множество, неизвестность. Поэтому и считается следующее за ним число 41 роковым.

В более позднее время число 40 перестало быть предельным, но сохранилось в пословицах, поговорках, сказках, обрядах. Поминки у славян происходят на сороковой день. По поверью, убить паука - значит избавиться от 40 грехов.

Кстати, название «сороконожка» означает вовсе не то, что у нее сорок ног, а то, что их множество. У других народов это же насекомое называется «тысяченожка».

Вот на таких искусственных выкладках зачастую и строились предсказания и пророчества.

Идут века, исчезают царства и целые народы, а вместе с ними отходит в прошлое их культура. Наука не стоит на месте, и то, что когда - то было неопознанным и пугающим, становится понятным и само собой разумеющимся. Но в памяти сохранились поверья, и мы подчас еще верим в счастливую семерку и несчастливое число «тринадцать», забывая при этом, что за каждым суеверием стоит история.

Самым, пожалуй, загадочным и даже волшебным числом в математике является число ноль. С его особыми свойствами мы сталкиваемся уже в начальной и средней школе. На ноль нельзя делить. При первом знакомстве с числовой прямой, выясняется, что ноль не тождественен пустому множеству. Это число не только имеет свою координату на числовой прямой, но из него берут начало системы отсчёта. Можно сказать, что ноль является пограничной точкой, разделяющей положительные и отрицательные числа, направления вверх и вниз, вправо и влево, вперёд и назад .В волшебной сказке мы встречаемся с героиней, чьи характеристики напоминают нам характеристики этого числа. Она всегда живёт на границе двух миров, являясь как бы дверью между ними. Избушка Бабы Яги никогда не является составной частью тех миров, которые она разделяет, но всегда лишь – границей. Итак, избушка Бабы Яги – это точка посвящения. Недостойные либо не допускаются, либо гибнут. Достойные могут пересечь эту границу и вернуться обратно в материальный мир живыми.

О НУЛЕ 
Когда-то многие считали, 
Что нуль не значит ничего. 
И как ни странно, полагали, 
Что нуль совсем не есть число. 
Но на оси средь прочих чисел 
Он все же место получил. 
И все действительные числа 
На два разряда разделил. 
Коль нуль к числу ты прибавляешь, 
Иль отнимаешь от него, 
В ответе тотчас получаешь 
Опять то самое число. 
Попав, как множитель, средь чисел 
Он сводит мигом все на нет. 
И потому в произведении 
Один за всех несет ответ. 
А относительно деленья 
Во-первых, нужно помнить то, 
Что уж давно в научном мире 
Делить на нуль запрещено. 
Причина всем ведь очевидна, 
А состоит причина в том, 
Что смысла нет в таком делении 
Противоречье в нем само.

Если внимательно прочитать  народные сказки, то можно заметить, что практически каждая из них с помощью образного слова передаёт определённую математическую информацию.

«Поди туда – не знаю куда (это бесконечность), принеси то – не знаю что…(неизвестная переменная Х)

Занятие 2. Как математики рассказывают сказки. Математические сказки.

Из каких частей состоит сказка? Оказывается, ответ на этот вопрос можно сформулировать строго математически – для этого лишь нужно составить сказочное уравнение с картинками вместо переменных

Угадайте эти сказки!

ТРЕУГОЛЬНИК И КВАДРАТ

Жили-были два брата: 
Треугольник с квадратом 
Старший — квадратный 
Добродушный, приятный 
Младший — треугольный, 
Вечно недовольный. 
Стал расспрашивать квадрат: 
— Почему ты злишься, брат? 
Тот кричит ему: — Смотри, 
Ты полней меня и шире, 
У меня углов лишь три, 
У тебя же их четыре! 
Но квадрат ответил: — Брат! 
Я же старше, я — квадрат: 
Я сказал еще нежней: 
— Неизвестно, кто нужней! 
Но настала ночь, и к брату, 
Натыкаясь на столы, 
Младший лезет воровато 
Срезать старшему углы. 
Уходя сказал: 
— Приятных я тебе Желаю снов! 
Знать, ложился — был квадратным, 
А проснешься без углов! 
Но наутро младший брат 
Страшной мести был не рад. 
Поглядел он — нет квадрата, 
Онемел, стоял без слов... 
Вот так месть! Теперь у брата 
Восемь новеньких углов.

Сказки из книги «Добрая математика»

Замечательные математические сказки я нашла прочитав книгу «Добрая математика». В книге приведены не только сказки, но задаются вопросы для осмысления прочитанного.

Вот только 2 сказки из данной книги:

"Гордая цифра Один"

- Привет ракета! - воскликнула цифра Один, увидев остроносую ракету в небе. Я цифра - Один похожа на тебя! Ты одна в пустынном космосе и ничего не боишься! Я люблю считать тех, кто один! Тот, кто один, он самый важный!

- Я не одна, внутри меня космонавты, а вокруг – звезды, - возразила ракета с высоты.

- Цифра Один, пошли гулять, - позвала Единицу ее соседка цифра Два.

- Я хочу гулять одна. Тот, кто один он самый важный, - гордо ответила Единица. – В небе светит только одно солнце и у человека только одна голова.

- А ходит человек на двух ногах и делает все двумя руками, - возразила цифра Два.

- Самое главное в человеке, это его голова, — упрямо повторила Единица.

- Зато два глаза и два уха, — возразила Двойка. — Разве может голова хорошо работать без них?

Помоги цифрам решить, кто важнее: Единица или Двойка?

Беседа

• Как вы думаете, почему у человека один язык, но два уха и два глаза?

• Почему лучше один раз увидеть, чем сто раз услышать?

• Почему, когда куда-либо едешь один, дорога кажется длиннее?

• Какие события в жизни каждого человека случаются только один раз?

• Загадайте какой-либо предмет и расскажите, не называя свой предмет, как людям живется в доме, если у них этот предмет только один. Например: если в доме он один, то нельзя делать уроки, когда все кушают (стол). Если в доме он один, то на нем сидит самый пожилой (стул). Остальные угадывают, о каком предмете идет речь.

"О чем мечтает цифра Два"

Однажды цифра Два встретила лебедя и сказала ему:

- Я похожа на тебя, и мечтаю научиться летать.

- Я не хочу больше летать, - грустно ответил лебедь. – Моя лебедушка попала в силки охотника, и мне тоскливо без нее.

- Я помогу тебе освободить лебедушку, - пообещала Двойка.

Вскоре два прекрасных лебедя поклонились цифре Два и сказали:

- Спасибо за помощь, ты похожа на нас и такая же добрая как мы.

- Но я не умею летать, как вы, — вздохнула Двойка.

- Возьми от нас на память эти два белых перышка, они исполнят твое самое заветное желание, - предложил лебедь.

На следующий день цифра Два гордо парила в воздухе на двух больших крыльях.

- Лебеди подарили мне два перышка, но когда они улетели, перышки превратились в крылья, - взволнованно рассказала Двойка цифрам.

- Тот, кто мечтает летать, обязательно полетит, - решили цифры.

Как ты думаешь, о чем еще мечтает цифра Два?

Беседа

• Как вы думаете, куда Двоечка полетит в первую очередь на своих крыльях?

• Объясните смысл пословицы «За двумя зайцами погонишься, ни одного не поймаешь». Вспомните какие-либо два своих самых важных дела и расскажите, какое из них все-таки важнее и нужнее для вас.

• Когда о людях говорят: «Два сапога пара» или «как две капли воды»? Как вы думаете, должны ли друзья быть «как две капли воды», и почему?

• Почему говорят, что лентяй работает дважды?

Занятие 3 - 4. Задачи из сказок.

1. Отправляют героев сказок за тридевять земель в тридесятое государство

А где это государство? Оказывается рядом…

Решение: 3х9=27дней (27 дней – лунный месяц – время обращения Луны вокруг Земли)

3х10=30 дней (30 дней - период между двумя новолуниями).

Ответ: Тридевятое царство, тридесятое государство находится на расстоянии, равному месяцу пути.

2. В стихотворении про известную сказочную героиню Дюймовочку сказано:

«Удобно спать Дюймовочке

В спичечной коробочке,

И догадаться просто – какого она роста»

Задание: Вычислите рост Дюймовочки в современных единицах измерения.

3. В «Сказке о коньке – горбунке» кобылица обещала Иванушке

за своё освобождение награду:

«….Двух рожу тебе коней.

Да таких, каких поныне

Не бывало и в помине.

Да еще рожу тебе конька

Ростом только в три вершка».

Задание: Вычислите рост конька - горбунка в современных единицах измерения.

4.Три богатыря окружили Соловья-разбойника так, что все богатыри образовали треугольник. От Ильи Муромца до Алеши Поповича 5 метров, а до Добрыни Никитича на 4 метра больше, чем от Алеши Поповича до Добрыни Никитича. От Алеши Поповича до Добрыни Никитича на 2 метра меньше, чем до Ильи Муромца. Каков периметр треугольника?

Ответ: 15 метров.

5. Илья Муромец отправился за Соловьем-разбойником. Собственная скорость лодки Ильи Муромца 4,5 км/ч, скорость течения реки 2,5 км/ч. Найдите скорость лодки при движении по течению и против течения. Какой путь пройдет лодка по течению за 4 часа? Какой путь она пройдет против течения за 3 часа?

Ответ: скорость лодки по течению – 7 км/ч, против течения – 2 км/ч. По течению за 4 часа лодка пройдет 28 км, против течения за 3 часа – 6 км.

6. Площадь поля боя Змея Горыныча и Алеши Поповича 15 км², ширина поля 3 км. Найдите длину и периметр поля.

Ответ: длина поля – 5 км, периметр – 16 км.

7. Отправился Иван-царевич за Василисой Премудрой в царство Кощея Бессмертного. Дорога туда составляет 25 километров. Прошел он 1/5 часть от всего пути. Сколько километров осталось пройти Ивану-царевичу?

Ответ: 20 километров.

8. Отправился старый солдат из сказки «Каша из топора» на побывку домой. Был у него с собой мешок с хлебом. Сколько хлеба в мешке, если 1/4 часть составляет 5 кусков хлеба?

Ответ: 20 кусков хлеба.

9.Как главные герои измеряли рост удава? В сказке он составляет 38 попугаев, 5 мартышек или 2 слоненка. А так ли это на самом деле?

Используя, учебник по биологии и энциклопедию мы узнали, что средний рост попугая = 22см, мартышки 77см, слона 335см, удава 10м. Выполнив, несложные вычисления получаем, что в жизни длина 1 удава = 45 попугаям ( 1000 : 22=45) =13 мартышкам (1000 : 77= 13). 9 = 3 слонам (1000 : 335 =3) (Г.Остер « Зарядка для хвоста». Вывод: автор в своем произведении пренебрег точными данными).

10.Лиса Алиса и кот Базилио привели Буратино на пустырь - это Поле Чудес: если закопать золотые монеты, то на утро вырастет дерево, на котором в 3 раза больше золотых монет. Затем полученные монеты можно снова закопать в землю и снова вырастет дерево с монетами. Так можно снять несколько урожаев. Они предложили посторожить ночью монеты. В награду за услугу лиса и кот потребовали отдавать с каждого урожая 9 монет. Подумав немного, Буратино не согласился с их требованиями. Он заявил, что после двух урожаев у него совсем не останется денег. Уж лучше он сам посторожит. Сколько золотых монет было у Буратино? А.Н. Толстой «Буратино».

Решение: Второй урожай дает 9 монет, значит во второй раз Буратино посадит 9: 3=3 (монеты). Первый урожай дал 3+9=12 (монет). Значит, в первый раз Буратино посадил 12: 3=4 (монеты)

11.Поросята Ниф-Ниф и Нуф-Нуф бежали от Волка к домику Наф-Нафа. Волку бежать до поросят (если бы они стояли на месте) 4 минуты. Поросятам бежать до домика 6 минут. Волк бежит вдвое быстрее поросят. Успеют ли поросята добежать до домика Наф-Нафа?

Решение: Волку бежать до домика Наф-Нафа 4 + 6: 2=7 минут.6 минут меньше, чем 7 минут. Значит, поросята успеют добежать до домика Наф-Нафа.

12. «Винни-Пух и его друзья». Решили Винни-Пух, Кролик и Пятачок купить горшочек мёда стоимостью 24 рубля. У Винни-Пуха с Кроликом было 20,6 р., у Винни- Пуха с Пятачком 12,9р., а у Кролика с Пятачком 18,5 р. Купят ли они горшочек мёда, если сложат все свой деньги? Сколько денег имел каждый?

Решение. 1. 20,6 + 12,9 + 18,5 = 52 (р) – удвоенная сумма денег Винни-Пуха, Кролика и Пятачка. 2. 52:2=26 (р) было у Винни-Пуха, Кролика и Пятачка вместе. 3. 26-20,6=5,4 (р) - у Пятачка. 4. 26-12,9=13,1 (р) – у Кролика. 5. 26-18,5=7,5 (р) – у Винни-Пуха.

Занятие 5 - 6. Сказочные герои в математических задачах.

Задача 1. Окружность колобка = 32 см. Он делает 100 оборотов в минуту. Сколько прокатился колобок до встречи с зайцем, если он катился 3 минуты?

Решение. Надо 32 умножить на 100. Получится 3200 см, то есть 32 м. Затем умножаем 32 на 3. Получится 96 м. Столько колобок прокатился до встречи с зайцем.

Задача 2.Курочка Ряба в первый, второй и третий день снесла одинаковое количество яиц, а в четвёртый снесла 2 яйца. Сколько яиц снесла курочка в каждый из этих дней, если всего она снесла пять яиц. Решение.

3х + 2 = 5 3х = 5 – 2 3х = 3 Х = 3:3 Х = 1 В каждый из трёх дней курица снесла по одному яйцу.

Задача 3. Маша бежала до печки восемь минут, до яблони пять минут, до речки шесть минут и до домика бабушки - яги десять минут. Сколько времени бежала Маша до домика?

Решение. 8 + 5 + 6 + 10 = 29 минут. Маша бежала до домика бабы яги 29 минут.

Задача 4. Собираясь убежать от медведя, Маша сделала 5 пирожков с грибами, 7 пирожков с мясом и несколько пирожков с яблочным вареньем. Сколько пирожков с яблочным вареньем приготовила Маша, если количество пирожков с яблочным вареньем равно сумме пирожков с грибами и пирожков 11

Решение. 5 + 7 = 12 пирожков с яблочным вареньем. Маша испекла 12 пирожков с вареньем.

Задача 5. Колобок. Жили - были старик со старухой. Замесила как-то старуха муку на сметане, состряпала Колобок, изжарила его в масле и на окошко студить положила.

Колобок полежал, взял и покатился. С окна на лавку, с лавки на пол, по полу к двери, прыг через порог и во двор. Со двора за ворота и дальше по тропинке в лес. В это время Лиса грелась у своей норы на расстоянии 40 км от Колобка, Заяц чистил морковку на расстоянии 30 км, а голодный Волк мечтал о еде на расстоянии 28 км. Уловив запах свежей выпечки, они одновременно помчались навстречу ему. Лиса бежала со скоростью 7 км/ч., Заяц со скоростью 6 км/ч., Волк со скоростью 4 км/ч. Кто первым встретился с Колобком, если он катился со скоростью 1 км/ч?

Решение. 1) находим скорости сближения зверей с Колобком:

7-1= 6км/ч - с Лисой

6-1= 5 км/ч - с Зайцем

4-1= 3км/ч - с Волком

2) 40:6 = 6 ч 40 мин - предполагаемое время встречи Лисы с Колобком

30:5 = 6 ч- предполагаемое время встречи Зайца с Колобком

28:3 = 9 ч 20 мин - предполагаемое время встречи Волка с Колобком

Ответ: первым с Колобком встретился Заяц

Задача 6. Золотая рыбка. Жил старик со своей старухой. Старик ловил рыбу, старуха пряла пряжу. Раз старик кинул невод в море. Пришел невод с травой морскою, второй раз кинул, пришел невод с одной тиною, но старик не расстраивался. Бросал невод в море он полтора часа, пока не поймалась золотая рыбка: три раза через каждые 10 минут, после каждые пять минут. Сколько раз старику пришлось бросить невод в море, прежде чем поймать золотую рыбку?

Решение:

1) 10 х 3= 30 мин

2) 1 час = 60 мин. 60:5= 12 раз

3) 12+3= 15 раз

Ответ: старик бросал невод в море 15 раз, прежде чем поймал рыбку.

Задача 7. Баба Яга. Баба Яга утверждает, что Змей Горыныч не пролетит 1000 км без дозаправки. Кощей Бессмертный поспорил с ней на бочку меда, что пролетит. Змей Горыныч пролетел 4 часа со скоростью 247 км/ч и, совершив вынужденную посадку, съел Ивана Царевича. Проспорила Баба Яга бочку меда или не проспорила?

Решение: за 4 часа Змей Горыныч пролетел 247 х 4 = 988 км

Ответ: Баба Яга не проспорила.

Задача 8. Сивка - бурка.В некотором царстве, в некотором государстве жил- был старик и было у него три сына. Младшего все Иванушкой-дурачком звали. Однажды собрались братья ехать к царскому двору, посмотреть на Елену Прекрасную. Иванушку с собой не взяли. Сели на коней и поехали. По 12 верст в день. А Иванушка вышел в тот же день и шел так: в первый день прошел 1 версту, во второй день – две версты, в третий – 3 версты и так, прибавляя каждый день по одной версте. Через сколько дней он настиг братьев, которые к тому времени уже дошли до дворца, и покорил сердце Елены Прекрасной?

Решение: в первый день Иванушка отстанет на 12 -1 = 11 верст, во второй еще на 12 – 2 = 10 верст, в третий еще на 12 -3=9 верст и так далее. На 12-й день отставание составит ( 11+10+9+…+2+1+0) верст.

А затем расстояние между ними начнет сокращаться. В 13 –й день на 13-12=1 версту, в 14-й день еще на 14-12=2 версты, в 15-й день еще на 15-12=3 версты и наконец, в 23 –й день на 23-12 = 11 верст. На 23 –й день расстояние между ними уменьшится на (1+1+3+…+10+11) верст.

Ответ: Иванушка догонит братьев по прошествии 23 дней.

Задача 9. Хаврошечка. Жила - была семья, и росли в семье три дочери одна другой ленивей. Взяли они в свой дом сиротку, Крошечку-Хаврошечку. Она их обшивала, для них пряла и ткала и слова доброго никогда не слыхивала. Совсем заморили ее работой.

Пожаловалась Крошечка-Хаврошечка на свое житье любимой коровушке. А коровушка ей в ответ: «Красавица – девица, влезь ко мне в ушко, а в другое вылези, все будет сработано». Так все и сбывалось. Отнесет она хозяйке рулоны сукна, та их спрячет и еще больше работы задаст. Набрался у хозяйки целый сундук сукна, и решила она его продать. Разложили они около дома разноцветные рулоны сукна. 20 рулонов белого сукна, 13 рулонов черного сукна, 5 красного, 19 зеленого и 7 синего. А в то время ехал мимо молодой богатый купец. Залюбовался он красивым товаром и решил купить. А дочери с ним так и заигрывают. Заплатил купец за все рулоны 486 рублей. Цена рулонов была не равная: за черный рулон он платил на 4 рубля больше, чем за белый, за красный – на 3 рубля меньше, чем за черный, за зеленый на 2 рубля меньше, чем за красный, а за синий на 1 руб. больше, чем за зеленый. Сколько денег он заплатил за один рулон каждого цвета? Этот вопрос он задал хозяйским дочерям. Долго думали девицы, но ни одна из них не смогла ответить. Только Крошечка-Хаврошечка несмело ответила на вопрос купца. Услышав правильный ответ, он обрадовался и увез ее с собой. Так и стали они жить вместе в добре и лиха не знать.

Решение: (способ 1)

Легко видеть, что самое дешевое сукно зеленое, синее стоит дороже его на 1 рубль , красное на 2 рубля, черное на 5 рублей, белое на рубль. Если бы за каждый вид сукна было уплачено столько же сколько за зеленое, то при этом было бы уплачено меньше на 20 х 1 + 13 х 5 + 5 х 2 + 7 х 1 = 102 рубля. Вся покупка стоила бы 486 – 102 = 384 рубля. А так как куплено 64 рулона сукна, то рулон зеленого сукна стоит 384: 64 = 6 рублей. Зная это, легко находим стоимость остальных рулонов. 6+1=7 рублей- синее сукно; 6+2=8 рублей- красное сукно; 8+3=11 рублей-чёрное сукно; 11-4=7 рублей- белое сукно.

Решение: (способ 2)

Пусть один рулон белого сукна стоит Х рублей. Черного - (Х + 4) рублей, красного -(Х+1)рублей, зеленого -(Х-1) рублей, синего- Х рублей. Тогда 20 Х + 13 (Х+4) + 5 (Х+1) + 19 (Х-1) + 7Х = 486. Решив уравнение получаем, что один рулон белого цвета стоит 7 рублей, черного – 11 рублей, красного – 8 рублей, зеленого – 6 рублей, синего – 7 рублей.

Занятие 7-8. Старинные меры счисления. (2 часа)

В русской литературе, говоря о каком-то персонаже, писатели нередко указывали старинные меры длины.  Большинство старых мер забыто, вышло из употребления, но многие из них есть в литературных произведениях, исторических памятниках. Меры жили, иногда старились и умирали, иногда возрождались к новой жизни. История мер – это часть истории человечества.

 В качестве единицы измерения объема на Руси использовалась подручная домашняя утварь.  Основные русские  меры объема жидкостей – ведро, бутыль, кружка, чарка, шкалик, бочка. 

   Русский народ использовал такие меры веса как пуд, полпуда, золотник, безмен, кадь.

   В ходу были денежные меры: алтын, гривна, грош, полтина, пятак, полушка.                                         

 Аршин - мера аршин  вошла в употребление в результате развития торговли с восточными народами (от персидского арш – локоть). Он  равен 71 см 12 мм. Пришёл он на Русь вместе с купцами из далёких стран. Восточные купцы, отмеряя ткани, обходились без всяких метров: ткань они натягивали на собственную руку, до плеча. Это и называлось мерить аршинами. 

Мера была хоть и очень удобной, но был у неё существенный недостаток: руки, к сожалению, у всех разные. Хитрые купцы быстро соображали, что нужно искать приказчиков с руками покороче: тот же  кусок, а аршинов больше. Но однажды этому пришёл конец. Продавать «на свой аршин» властями было строжайше запрещено. Употреблять разрешалось только казённый аршин.

 Казённый аршин – линейку, длиной в чью-то руку, - изготовили в Москве, потом с него сделали копии и разослали во все концы России. Чтобы деревянный аршин нельзя было укоротить, концы его оковали железом и пометили печатью.

 Десятки лет уже не измеряют аршинами, но слово это не забыто. До сих пор в пословицах и поговорках мы встречаем эту меру длины.

Например:

 На три аршина в землю видит!  – о внимательном, прозорливом человеке, от которого ничего невозможно утаить.

Меряет на свой аршин . Каждый купец на свой аршин меряет – о человеке, который судит все односторонне, исходя из собственных интересов.

Аршин на кафтан, да два на заплатки. 

Писать о чужих грехах аршинными,  а о своих  - строчными буквами.

Сидит, ходит, словно аршин проглотил  – о неестественно прямом человеке.

На аршин борода, да ума на пядь – о взрослом, но глупом человеке.

Пишешь аршинными буквами – очень крупно.

В авторских произведениях данная мера встречается довольно часто.

   А.С. Пушкин « Сказка о царе Салтане, о сыне его славном и могучем богатыре князе Гвидоне Салтановиче и о прекрасной Царевне Лебеди» -

Между тем, как он далеко

Бьется долго и жестоко,

Наступает срок родин;

Сына бог им дал в аршин.

   П.П.Ершов «Конек-горбунок» -

На спине с двумя горбами

Да с аршинными ушами.

   Ф.И.Тютчев -
Умом Россию не понять,

Аршином  - не измерить.

   Н.А.Некрасов « Дед Мазай и зайцы» -

С каждой минутой вода подбиралась
К бедным зверькам;
Уж под ними осталось меньше аршина земли в ширину…

   Верста - русская путевая мера. Первоначально - расстояние от одного поворота плуга до другого во время пахоты. Длина версты 1060 м. 
  Коломенская верста – «верзила» - шутливое название очень высокого человека [1,60]. Оно берет свое начало от времен царя Алексея Михайловича, царствовавшего с 1645 по 1676 г. 

   Межевая верста существовала на Руси до 18 в. Для определения расстояния между населенными пунктами  и для межевания (от слова межа - граница земельных владений в виде узкой полосы). Длина такой версты 1000 саженей, или 2,13 км.

Данная мера встречается часто в произведениях разного жанра.

Москва верстой далека, а сердцу рядом - так русские люди характеризовали свое отношение к столице.                                                                                                                              

Любовь не верстами меряется [1,60]. Сто верст молодцу не крюк - расстояние не может быть препятствием для любви.                                                                                                                               От слова до дела - целая верста.                                                                                                     

Верстой ближе - пятаком дешевле.                                                                                                            На версту отстанешь - на десять догоняешь - даже небольшое отставание очень трудно преодолевать.  

Его  за версту видно – хорошо приметный человек.

Врать - семь верст до небес и все лесом . 
За семь верст комара искали , а комар на носу. 
От мысли до мысли пять тысяч верст. 
Охотник за семь верст ходит киселя хлебать[1,31].

Тянись верстой, да не будь простой. 

   Былина «Вольга Святославович» -

Обернулся тут Вольга гнедым туром с золотыми рогами и побежал к Индийскому царству: первый прыжок сделал – за версту ушел, а со вторым из вида скрылся.

   Русская сказка «Бой на калиновом мосту» -

Выезжает Чудо-Юдо шестиглавый змей,
как дыхнет на все стороны –
на три версты все огнем пожег.

   А.С.Пушкин «Зимняя дорога» -  

Ни огня, ни черной хаты
Глушь и снег навстречу мне.
Только версты полосаты
Попадаются одне.

   Н.А.Некрасов «Генерал Топтыгин» -

А коням подавно страх-

Не передохнули!

Верст пятнадцать во весь мах

Бедные отдули!

   П.П.Ершов «Конек-горбунок»  -

Горбунок летит, как ветер,
И почти на первый вечер
Верст  сто тысяч отмахал,
И нигде не отдыхал.

   Вершок - старинная русская мера длины, равная  ширине двух пальцев (указательного и среднего).

   Вершок равнялся 1/16 аршина, 1/4 четверти. В современном исчислении - 4,44см. Наименование "Вершок" происходит от слова "верх".

   В литературе мы часто встречаемся с этой мерой.

 Например:

От горшка два вершка, а уже указчик [1,61] - молодой человек, не имеющий жизненного опыта, но самонадеянно поучающий всех.

У нее суббота через пятницу на два вершка вылезла – о неаккуратной женщине, у которой нижняя рубашка длинней юбки.

   П.П.Ершов «Конек горбунок» -  

По исходе же трех дней,
Двух рожу тебе коней –
Да таких, каких поныне
Не бывало и в помине,
Да еще рожу конька, ростом только в три вершка
На спине с двумя горбами, да с аршинными ушами

   Сажень (от сягать – доставать до чего-либо, достигать) относится к XI  веку.

В быту существовали разные сажени – маховая и косая. Итак,

   Маховая – расстояние между раскинутыми в обе стороны руками по концы вытянутых средних пальцев; 1 маховая сажень – 1м 76 см.

Косая – от каблука правой ноги до кончиков пальцев вытянутой вверх левой руки, т.е. около 248 см. 

   Иногда о человеке говорят: «В плечах – косая сажень» [1,406].  

Вот примеры использования этой меры в произведениях:

Ты от правды (от службы) на пядень, а она от тебя – на сажень.

   Н.А.Некрасов « Дед Мазай и зайцы» -

С каждой минутой вода подбиралась
К бедным зверькам;
Уж под ними осталось меньше аршина земли в ширину,
меньше сажени в длину.

   Былина «Алеша Попович и Тугарин» -  

Видел я Тугарина Змеевича.

В вышину ли он, Тугарин, трех сажень.

Промеж глаз калена стрела.  

Пядь (или пядень[1,373]) - старинная мера длины, равная примерно четверти аршина, то есть четвертой части от 71,1 см. Несложные расчеты показывают, что в пяди было около 18 сантиметров.

   Древнерусское "пядь" восходит к общеславянскому глаголу "пяти" - растягивать. Поэтому встречаются такие выражения:

Не уступить ни пяди - не отдавать даже самой малости.

Семь пядей во лбу [1,373] - об очень умном человеке.

Локоть – расстояние по прямой от локтевого сгиба до конца вытянутого среднего пальца руки.  

Локоть широко применяли в торговле как особенно удобную меру. В розничной торговле холстом, сукном, полотном –локоть был основной мерой. Недаром говорили: «Сам  с ноготок, а борода с локоток»

1. Собакевич – Чичикову: «А Пробка Степан, плотник? Я голову про закладную, если вы где сыщете такого мужика. Ведь что за силища была! Служи он в гвардии, ему бы бог знает что дали, трех аршин с вершком ростом!» (Н.В. Гоголь, «Мертвые души»). 

2. «Из числа всей ее челяди самым замечательным лицом был дворник Герасим, мужчина 12 вершков роста, сложенный богатырем и глухонемой от рожденья» (И.С. Тургенев, «Муму»). 

3. «Никитушка Ломов, бурлак, ходивший по Волге лет 20-15 тому назад, был гигант, геркулесовской силы; 15 вершков ростом…» (Н.Г. Чернышевский, «Что делать?»). 

Кто из упомянутых литературных персонажей самый низкий, а кто самый высокий? Какова у этих двоих разница в росте?

Решение.

Ответ: Самый низкий – Герасим, самый высокий – Пробка Степан. Разница – 22 см.

* В старину рост человека часто определялся в вершках свыше обязательных для нормального взрослого человека двух аршин, то есть 1м 42 см.

4. Герой стихотворения Н.А. Некрасова «Дедушка Мазай и зайцы» вспоминает о том, как в половодье зайцев спасал:

Вижу один островок небольшой –

Зайцы на нем собралися гурьбой.

С каждой минуты вода подбиралась

К бедным зверькам; уж под ними осталось

Меньше аршина земли в ширину,

Меньше сажени в длину.

Насколько мал был тот островок?

Каковы его максимальные размеры в современных единицах длины и площади?

5.«Охотник и Чукля».

«Старичок- боровичок и говорит охотнику: -Твоя беда – в твоей зависти, мил человек. Помни: в чужих руках золотник велик, а как нам достанется, мал покажется. Что ты добыл, всё Чукля проглотил. Теперь только на свою удачу надейся.»

* Золотник – мера веса ( равен 4,26гр.)

6.«Фома»

«Удивляется царь, радуется: такое богатство с неба свалилось! Хвалит Фому, царские приветы ему с лисой шлёт. Фома ж про то и не ведает, знай на печи похрапывает да посвистывает. А лиса своё дело знает. Приходит к царю, и говорит: - Фома просил у тебя пудовку – деньги мерить. А то, говорит, пересчитывать долго…»

* Пудовка – берестяная пудовая мерка для зерна, вмещает пуд ( равен 14,4кг)

Занятие 9. Математики – литераторы

Почему среди математиков оказывается так много талантливых писателей? Казалось бы, буйная фантазия и строгая цифра - вещи несовместимые, присущие антиподам. Но как объяснить феномен Льюиса Кэрролла, Александра Солженицына, Софьи Ковалевской, Александра Сухово-Кобылина, Айзека Азимова, нашего современника Александра Кабакова, не говоря о фигурах меньшей известности? Слишком много имен, чтобы это было случайностью. В канадском университете Ватерлоо проведено исследование, которое доказывает, что вслед за проявившимися в детстве способностями хорошего рассказчика обнаруживаются и яркая математическая одаренность.

ПУШКИН И МАТЕМАТИКА.

Прослеживается неразрывная связь Пушкина с математикой. Первые знания по математике Пушкин получил, скорее всего, в детстве от часто сменяющихся французов-гувернеров.

В лицее математику изучали основательно: в программу математики входили арифметика, геометрия, прикладная математика, чистая математика, даже математика с дифференциалами и интегралами. Но, Пушкин в лицее “ленился и отставал”. Тем не менее, я считаю, что Пушкин получил неплохую математическую подготовку.

Поэтому впоследствии в его творчестве находятся некоторые интересные моменты, связанные с математикой

Кое-какие данные, связанные с расчетами имеются в сказке “ О царе Салтане”. Просчитав возможное расстояние от царства Салтана до острова Буяна, до города-дворца, обоснованного князем Гвидоном, до которого могла доплыть бочка с царицей и его сыном, сделал вывод, что царица с сыном находились на достаточно большом расстоянии, что весть о диковинках этого города доходила до царя Салтана проезжающих купцов не так быстро и не так долго.   Значит, поэзия Пушкина базировалась на глубоком знании предмета, охвате всех его сторон и оказалась достовернее упрощенных примитивных математических моделей. 
Значит, слова “Сказка ложь, да в ней намек, добрым молодцам урок”- непустые слова в сказках Пушкина. Кроме того, крылатые слова Пушкина “В геометрии нужно вдохновение, как и в поэзии”, “Поверил я алгеброй гармонию” и др. имеют глубокий математический смысл.

А.П. ЧЕХОВ "ЗАДАЧИ СУМАСШЕДШЕГО МАТЕМАТИКА"

- За мной гнались 30 собак, из которых 7 были белые, 8 серые, а остальные черные. Спрашивается, за какую ногу укусили меня собаки, за правую или левую?  

- Куплено было 20 цибиков чая. В каждом цибике было по 5 пудов, каждый пуд имел 40 фунтов. Из лошадей, везших чай, две пали в дороге, один из возчиков заболел, и 18 фунтов рассыпалось. Фунт имеет 96 золотников чая. Спрашивается, какая разница между огуречным рассолом и недоумением? 

- Английский язык имеет 137856738 слов, французский в 0,7 раз больше. Англичане сошлись с французами и соединили оба языка воедино. Спрашивается, что стоит третий попугай и сколько понадобилось времени, чтобы покорить сии народы? 

- В среду 17-го июня 1881 года в 3 часа ночи должен был выйти со станции А поезд железной дороги, с тем, чтобы в 11 час. вечера прибыть па станцию В; но при самом отправлении поезда получено было приказание, чтобы поезд прибыл на станцию В в 7 часов вечера. Кто продолжительнее любит, мужчина или женщина? 

- Моей теще 75 лет, а жене 42. Который час?

Литературно – Математическая викторина

• ¥ Какому русскому поэту принадлежат эти математические строки: «Мы почитаем всех нулями, а единицами себя»? (А.С. Пушкину.)

• ¥ Какой пушкинский герой говорил:

«... Поверил

Я алгеброй гармонию...»

(Сальери в произведении «Моцарт и Сальери».)

• ¥ Чьи это строки?

«Мы любим всё - и жар холодных чисел,

И дар божественных видений,

Нам внятно всё - и острый галльский смысл,

И сумрачный германский гений...»

(А. Блок «Скифы».)

• ¥ Какой поэт воспел числа?

«Вам поклоняюсь, вас желаю, числа!

Свободные, бесплотные, как тени,

Вы радугой связующей повисли

К раздумиям с вершины вдохновенья!»

(В. Брюсов «Числа».)

• ¥ Какие книги написал профессор математики, логик Чарльз Лютвидж Доджсон, он же Льюис Кэррол?

(«Алиса в стране Чудес», «В Зазеркалье».)

• ¥ Что изобрёл Льюис Кэрролл как математик?

(Способы проверки делимости чисел на 17 и 19. Приём запоминания ряда цифр бесконечной дроби 3,14..., благодаря которому он мог записать число p до 71 знака после запятой. Предвосхитил некоторые идеи математической логики.)

• ¥ Сколько жителей было в деревушке Флорида штата Миссури, в которой родился будущий писатель Марк Твен, если в автобиографии писатель говорит: «Я увеличил население ровно на один процент. Не каждый исторический деятель может похвастаться, что сделал больше для родного города»? (100 человек.)

• ¥ В повести И.С. Тургенева «Муму» сказано, что Герасим был «двенадцать вершков роста». Один вершок примерно равен 4,4 см. Получается, что рост Герасима был около 53 см, что противоречит описанию могучей фигуры героя в повести. Разве у Тургенева было плохо с математикой? (Нет. Просто во времена Тургенева указывалось, на сколько вершков человеческий рост превышает 2 аршина. Один аршин равен 71 см, поэтому настоящий рост Герасима 195 см.)

• ¥ Какое число получило имя Шахерезады (Шехерезады) и каковы его замечательные свойства? (1001 - число Шахерезады, оно виднеется в заглавии бессмертных сказок «Тысяча и одна ночь». С точки зрения математики число 1001 обладает целым рядом интереснейших свойств:

а) Это самое малое натуральное четырёхзначное число, которое можно представить в виде суммы кубов двух натуральных чисел: 1001 = 103+13;

б) Число 1001 состоит из 77 злополучных чёртовых дюжин (1001 = 77х13), из 91 одиннадцаток или из 143 семёрок (вспомним, что число 7 считалось магическим числом);

в) На свойствах числа 1001 базируется метод определения делимости числа на 7, на 11 и на 13.)

• ¥ Какой прозаический жанр является средним арифметическим рассказа и романа? (Повесть.)

• ¥ Рекордсменом среди писателей с результатом 27000 является Л.Н. Толстой, а на втором месте - А.С. Пушкин с 24000. По какой номинации?

(По запасу используемых слов.)

• ¥ По подсчётам учёных, герои произведений Шекспира произносят это слово 2259 раз. Что это за слово? («Любовь».)

• ¥ «Математический» детский фольклор - это ... Что? (Считалки, считалочки.)

• ¥ Какая «литературная величина» произведения бывает и положительной, и отрицательной? (Герой, персонаж литературного произведения.)

• ¥ Какую линию можно найти в литературном произведении? (Сюжетную линию.)

• ¥ Что любят делать «делимым» у неубитого медведя, согласно русской пословице? (Шкуру. Делить шкуру неубитого медведя.)

• ¥ Какой математический закон, известный всем с младших классов, стал популярной пословицей? (От перемены мест слагаемых сумма не изменяется. Это переместительный, или коммутативный закон, свойство сложения и умножения, выражаемое формулами a + b = b + a, ab = ba.)

• ¥ Кто выше: сказочный россиянин-коротышка Мужичок-с-ноготок или Дюймовочка? (Дюймовочка, ведь рост Дюймовочки 2,54 см, что больше размера ноготка.)

Занятие 10. Задачи – один из видов народного творчества.

В нашем народе издавна популярен один из видов народного творчества - это задачи, относящийся к различным житейским ситуациям. Они были в ходу наряду со сказками, пословицами и загадками. Основная цель этих задач была не столько забавлять, а сколько проверять способность людей к остроумным рассуждениям, уровень их сообразительности и находчивости. Условия и решения этих задач доставляли не меньше удовольствия, чем исполнение народных песен и танцев и рассказывание сказок. Эти задачи не имели авторов и распространялись в устной форме. Они были плодом народного творчества.

Рассмотрим некоторые из них.

1. Дед, отец и сын встретили во время прогулки знакомого, который спросил, сколько каждому из них лет. «Нам 131 год и 10 месяцев», - ответил за всех дед и важно зашагал вперед. Тогда их знакомый, продолжая интересоваться их возрастом, спросил отца: «Ну скажите же, сколько вам лет?» - «Мне вместе с сыном 57 лет и 2 месяца,- ответил отец,
   - а сын на 19 лет и 10 месяцев моложе меня». Так знакомому и не пришлось узнать, сколько лет каждому из них.
   Сколько лет деду, отцу и сыну?
   Ответ: Деду-74 года и 8 месяцев, отцу-38 лет и 6 месяцев, сыну-18лет и 8 месяцев.

2. Человеку необходимо было переправить через реку с помощью лодки волка, козу и капусту. В лодке могли поместиться только человек, а с ним или волк, или коза, или капуста. Но если оставить волка с козой без человека, то волк съест козу. Если оставить с козой капусту, то коза съест капусту, а в присутствии человека, никто ничего не ест. Человек всё -таки перевёз через реку и волка и козу и капусту. Как он это сделал?

 Ответ: сначала переправится с козой, потом перевезёт капусту, но, возвращаясь берёт с собой козу, оставляет её на первом берегу, перевезёт волка, потом придёт за козой.

3. Купец купил 138 аршин черного и синего сукна на 540 руб. Спрашивается, сколько аршин купил он того и другого, если синее стоило 5 рублей за аршин, а черное - 3 рубля.
   Решение:
   Пусть синего сукна было х аршин, тогда черного (138-х) аршин. 
   5х+3(138-х)=540 
   5х+414-3х=540 
   2х=126 
   х=63(аршина) - синего 
   138-63=75(аршин) черного. 
   Ответ: синего 63 аршина, черного 75 аршин.
   
   * Аршин – старинная мера длины (равна 71 см).

4. На одном дереве сидело 40 сорок. Пришёл охотник, выстрелил и убил 6 сорок. Сколько сорок осталось на дереве?

Ответ: ни одной, остальные улетели.

5. Можно ли двумя монетами, один из которых не пятак заплатить за товар стоимостью 55 копеек.

Ответ: да, 50=5+55.

6. Рыбак ловил рыбу. На вопрос, сколько он поймал рыбы? - он ответил: «Половину восьми, 6 без головы, 9 без хвоста». Сколько рыбы поймал рыбак?

Ответ: 0.

7. Высота сосны 20 м. муравей ползёт по нему и поднимается за день на 5м вверх и за ночь опускается на 4м вниз. За сколько дней муравей доползёт до вершины столба?

Ответ: за 16 дней. (В первые 15 дней поднимается на 15м, на 16 день ещё на 5м.)

8. Летела стая гусей, а навстречу им летит один гусь и говорит: «Здравствуйте сто гусей!» Старший гусь, их вожак, ответил: «нас не сто гусей. Но если взять сколько есть, да ещё столько, да ещё пол столько, да ещё четверть столько, да ещё вместе с тобой,- нас будет сто». Сколько было гусей?

Ответ:36 гусей.

Интересно старинное решение этой задачи: Итак, полетел одинокий гусь дальше, и всё думал, сколько гусей встретил. Но сколько ни думал, так и не смог решить задачу.

Тут увидел гусь на берегу реки аиста. А аист пользуется среди других птиц славой математика: по целым часам иногда стоит неподвижно на одной ноге и всё думает, видно задачи решает. Слетел гусь на озеро, подплыл к аисту, выразил к нему своё почтение и рассказал аисту, какую задачу задал вожак, а он никак не может её решить. Подумал аист и предложил найти решение общими усилиями. Хорошо рассуждал аист и ловко использовал свой длинный клюв. На песке начертил одну черту, потом другую, такую же, потом половину, затем четверть черты и поставил в конце точку.

С завидным терпением объяснял аист, что этот рисунок точно соответствует ответу старого гуся о числе гусей в стае. А точка, это тот самый гусь, который ходит возле аиста и думает, мудрую думу. Тогда остальные чёрточки – 99 гусей. Найдём сколько четвертей во всех чёрточках вместе: 1+2+4+4=11. Итак, 11 четвертей. Тогда одна четверть: 99:11=9. Значит 9*4=36 гусей.

Гусь обрадовался, что вместе с аистом решили задачу. А аист важно вздохнул: «Эх ты, гусь, гусь…»

Фольклорные задачи характеризуют жизнь людей. Задачи эти воспрещают занятия людей, пеших путников на дорогах, Освещение улиц тусклыми керосиновыми фонарями т. д.

9. Некто, желая раздать нищим деньги рассчитал, что если каждому дать по 15 копеек, то у него не хватит 10 копеек, а если дать каждому по 12 копеек, то останется 14 копеек. Сколько было нищих, и сколько было у него денег?

Ответ:8 нищих, 110 копеек.

10. Гончар продавал глиняную посуду. Старушка купила один кувшин, за который заплатила 1 руб. и ещё пол кувшина. Сколько стоит кувшин?

Ответ: 2 рубля.

Занятие 11. Геометрические фигуры в рисунках хоровода.

Русский народный танец - яркое, красочное творение народа, являющееся эмоциональным художественным отображением его быта, характера, мыслей, чувств и понимание красоты окружающего мира.

Селезень утку догонял,
Молодой серу догонял.
Пойди, утица, домой,
Пойди, серая, домой.

У тя семеро детей,
А восьмой селезень,
А девятая сама,
Поцелуй разок меня.

Самый распространенный и самый древний вид русского танца - хоровод.

Его основной композицией служит круг – символ солнца. Это хождение по кругу берет начало из древних языческих обрядов, поклонение богу солнца – Яриле. Тогда этот танец носил обрядовый характер, но со временем утратил его.

В хороводе неразрывно связаны пляски, игры, песни. Иными словами, участники играют, пляшут и поют, их может быть неограниченное количество.

Русские хороводы делятся на орнаментальные и игровые.

В орнаментальном хороводе танцующие ходят кругами, рядами, создают из хороводной цепи фигуры, в ритм с музыкой, которая является для них лишь музыкальным  сопровождением. В песне к такому хороводу нет яркого сюжета с действующими лицами, какого-то конкретного действия. Их содержание связано с образами природы, коллективным народным трудом, бытом.  Замысловатые фигуры хоровода имитируют узоры русских кружевниц, узоры, вырезанные по дереву, работу живописцев.

Второй вид русского хоровода – игровой. Главным в нем является раскрытие сюжета. В сопровождающей танец песне есть конкретное действие, герои,  и исполнители разыгрывают его с помощью пляски, жестов, мимики. Создают образы, характеры героев, изображают трудовые процессы, сказочные темы. Рисунки в игровых хороводах проще, чем в орнаментальных. Композиция строится по кругу, либо парами и линиями.

В рисунке хоровода легко увидеть геометрические фигуры:

- окружность,

- полукруг,

- квадрат,

- ромб,

- кривая и т.д.

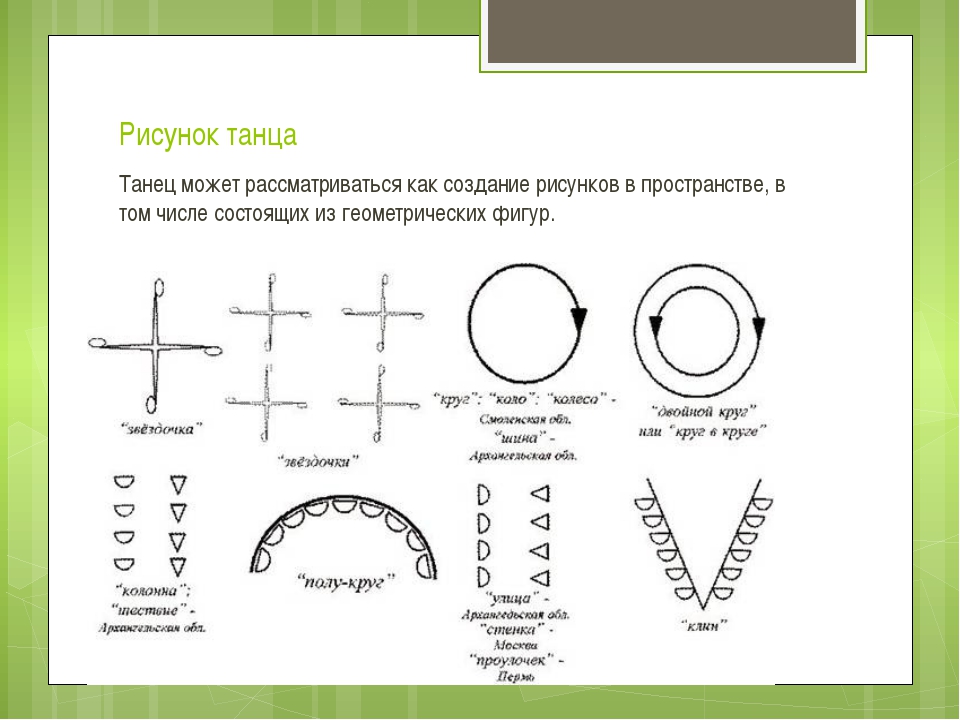
Основные фигуры хороводов.

Фигуры могут образовываться одними девушками, или одними парнями, или парнями и девушками вместе , которые могут быть выстроены в одну линию или соединены парами. Руки, соединены при построении фигуры, могут быть подняты вверх, раскрыты в стороны, опущены вниз и т.д.

«Круг»

Эту фигуру в Смоленской области называют «коло», «колесо», в Архангельской «шина». Число участвующих в этой фигуре не ограничено, однако их должно быть не менее трех человек. Парни и девушки повернувшись, лицом к центру круга и взявшись за руки, образуют замкнутый круг. Руки свободно, без напряжения отходят от корпуса под небольшим углом вниз или вверх. Движение по кругу в хороводе идет «посольно» - по солнцу, или, как сейчас принято говорить, по движению часовой стрелки. Сделав легкий полуоборот корпуса по ходу движения, парни и девушки идут простыми или переменными шагами, или переменным шагом с притопом, или другим каким-либо шагом.

«Два круга рядом»

Круги находятся на небольшом расстоянии друг от друга или совсем рядом. Каждый круг может двигаться как по направлению движения часовой стрелки так и против ее движения. повороты обоих кругов происходят одновременно или в одну, или в разные стороны.

Парни и девушки двигаются такими же шагами, как и в продвижении по кругу.

«Круг в круге»

Один круг большой, а внутри него поменьше. Внешний круг движется по солнцу, а внутренний может двигаться как по солнцу, так и в противоположную сторону.

«Корзиночка»

В Ярославской области эту фигуру называют «переплетенный круг». Фигура образуется из двух кругов – круг в круге. Внешний состоит из парней, внутренний из девушек. В кругах должно быть равное количество участников. Стоя лицом к центру, парни и девушки берутся за руки, образуя каждые свой круг. Сделав шаг к кругу девушек, парни поднимают соединенные руки девушек, причем партнерша находится справа от партнера. Образуется единый переплетенный круг – «корзиночка». Число пар, участвующих в построении этой фигуры, не ограничено, однако их должно быть не менее четырех.

«Корзиночка» движется различными шагами – или «гармошкой», или «припаданием» в любую сторону. Головы исполнителей в момент движения могут быть повернуты по ходу движения, к своим партнерам или же к центру круга. Руки исполнителей могут находиться не только внутри круга, но и с внешней его стороны, со стороны спины его участников. Такое перестроение происходит из образовавшейся уже фигуры – «корзиночка». Парни поднимают соединенные руки вверх и через головы опускают за их спины, на соединенные руки парней.

«Восьмерка»

Эта фигура образуется из двух кругов, стоящих рядом. Круги движутся в различные стороны. В определенный момент ведущие одновременно разрывают круги, и участники через одного переходят из одного круга в другой, их общее движение образует рисунок, похожий на цифру «8». Круги как бы переливаются один в другой. Руки разрываются только в момент перехода из одного круга в другой. Иногда участники за руки не держатся, а идут в своих кругах в затылок друг другу. В хороводах Архангельской области фигуру «восьмерка» часто исполняют парами, составленными из девушек, которые не держатся за руки. Количество участников в каждом круге должно быть одинаковым. «Восьмерку» лучше всего исполнять простыми или переменным шагом.

«Улитка»

В Московской области эта фигура называется – «улитка», в Рязанской – «капуста», «капустка», в Архангельской – «завивать кошечкой», в Пермской – «навивать нитку». Эта фигура образуется, или, как говорят, «навивается» или «завивается», из круга. Ведущий хоровода разрывает общий круг и, продолжая движение по спирали в том же направлении, но уже внутри круга, делает как бы новый круг, но меньший по диаметру, чем первый; затем он «завивает», заводит второй, третий круг по концентрической окружности. Круги становятся все меньше и меньше, а все идущие за хороводом точно повторяют рисунок его движения. Число кругов зависит от количества людей, участвующих в хороводе. «Капусту», «улитку» «завили». Теперь надо ее «развивать». Есть три варианта «развивания» этой фигуры, то есть возвращение в исходное положение.

1-й вариант. Продолжая движение, хороводник дает разворот влево на 180 градусов и начинает выводить хороводную цепь по образовавшемуся между кругами коридору. Движение идет постепенно увеличивающимися кругами до образования первоначального круга. Все идущие за ним точно повторяют рисунок его движения. «Завивает» хороводник «улитку» по движению часовой стрелки, по солнцу, а «развивает» ее против движения часовой стрелки.

2-й вариант. Хоровод останавливается, участники стоят лицом к центру круга. Хороводник пригнувшись, проходит под руками одной пары первого круга внутреннего круга, затем второго и так далее, пока не выйдет из последнего внешнего круга, ведя за собой хороводную цепь. Затем он делает поворот направо и продолжает двигаться по направлению движения первоначального круга. Так часто «развивают» «кошечек» в северных областях России.

3-й вариант. «Развивает» «капустку» второй хороводник, находящийся на другом конце хороводной цепи. Вся хороводная цепь начинает движение в обратном направлении, повторяя тот же рисунок, что и при «завивании». Круги идут по концентрической окружности, но постепенно увеличиваясь.

«Змейка»

В Архангельской области эту фигуру называют «кривули», в Московской – «уж». Фигура «змейка» может начинаться из линии, но чаще она является развитием круга. Ведущий хоровода, разорвав круг и продолжая двигаться внутри него, начинает делать повороты влево и вправо, подражая изгибам змеи. Все исполнители, на разрывая рук, следуют за ведущим. «змейка» исполняется в основном на площадке, занимаемой хороводом. Иногда «змейка» исполняется в основном на площади вокруг стогов или деревьев и т.д. Двигаться «змейка» может и медленно и довольно быстро, простым или переменным шагом, шагом с притопом и даже дробной дорожкой.

«Колонна»

В Архангельской области фигура называется «шествие». Это построение рядами. Каждый рад может состоять из нескольких человек, но не менее двух. В каждом ряду должно быть одинаковое количество участников, стоящих на небольшом расстоянии друг от друга. Ряды могут состоять как из парней и девушек, так и из одних девушек. Несколько рядов, находящихся на небольшом расстоянии друг от друга, и образуют фигуру «колонна». Ряды стоят в затылок один другому. «Колонна» представляет собой вытянутый прямоугольник, в котором ширина рядов всегда меньше длинны «колонны». Чаше всего в этом построении за руки не держатся. Самая маленькая «колонна»,где каждый ряд состоит из двух человек. Такое построение «колонной» в две линии в Архангельской области называется «застенок». «Колонна» движется чаще всего простым шагом.

«Улица»

В Московской области она называется «стенка», в Пермской – «проулочек», в Архангельской – «улица». Два ряда и две параллельные линии, стоящие на небольшом расстоянии лицом друг к другу, образуют фигуру «улица». Это две линии сходятся либо одновременно, либо одна линия может стоять, а другая идти на нее, либо одна линия может отступать, другая идти на нее. В одной линии могут стоять парни, а в другой девушки, линии могут быть смешанными. Чаще всего в этой фигуре участники держатся за руки и движутся простым шагом.

«Ворота»

Эта фигура носит также название «воротики», «воротца». Две линии исполнителей стоят парами одна против другой – «улицей».Пары одной линии берутся за руки и, подняв их вверх, образуют «ворота», другая рука свободно опущена вниз. Пары, стоящие, напротив в другой линии, простым или переменным шагом проходят под «воротами». Часто все пары одной линии, соединив руки и подняв их вверх, образуют непрерывные «воротики». Другая линия с разъединенными руками проходят по одному под каждые «воротики». Иногда исполнители, взявшись за руки, стоят в круге. Ведущий, разорвав круг, через центр ведет его за собой хороводную цепь. Подойдя к любой паре, он дает знак «поднять ворота». Одна пара поднимает руки, и исполнители проходят в образовавшиеся «воротца». Построение из «воротиков» бывает и такое: пары взявшись за руки, стоят по кругу. Одна половина пар стоит по направлению движения часовой стрелки, другая половина пар – против ее движения. Одновременно все пары начинают двигаться навстречу друг другу простым или переменным шагом по линии круга. Одна половина пар исполнителей образует «ворота», остальные пары проходят под ними. Продолжая движение по кругу, теперь уже другая половина исполнителей делает «ворота», а остальные пары проходят под ними.

«Гребень»

В Ярославской области эта фигура называется «прочес». Две линии исполнителей, выстроившись друг против друга «стенкой», движутся навстречу простым или переменным шагом. Руки исполнителей свободно опущены вниз. Обе линии встречаются и , продолжая двигаться, проходят сквозь линии правым или левым плечом. Линии меняются местами.

Занятие 12 - 13. Орнамент в математике.

Орнамент– это украшение изделия различными геометрическими, растительными и животными элементами.

Орнамент предназначен для украшения различных предметов (посуды, мебели, текстильных изделий, оружия) и архитектурных сооружений. Связанный с поверхностью, которую он украшает и зрительно организует, орнамент, как правило, выявляет и подчеркивает своим построением, формой и цветом конструктивные особенности предмета, природную красоту материала.

В народном творчестве, каждая национальная культура выработала свою систему орнамента - мотивы, формы, расположения на украшаемой поверхности, Поэтому часто по орнаменту можно определить, к какому времени и к какой стране относится то или иное произведение искусства.

Так, в орнаментах Древнего Египта наибольшее распространение нашли расти-тельные мотивы, и среди них особенно часто встречались листья и цветы лотоса.

Классическими стали наиболее распространенные древнегреческие орнаменты - меандр и акант.

Слово «меандр» происходит от названия очень извилистой реки в Малой Азии. Орнамент меандр как будто повторяет излучины этой прихотлвой реки. Акант - это род травянистого растения, распространенного в Средиземноморье. У него большие листья, красиво изогнутые стебли.

Орнаментальное искусство достигло совершенства на мусульманском Востоке. Для него характерно сочетание геометрических и растительных мотивов, так как Кораном было запрещено изображение людей и животных. Впоследствии, распространившись по Европе, этот вид орнамента получил название «арабеска» (от ит. arabesco - арабский), В исламских странах арабеска безраздельно господствует в архитектурном декоре.

Высокого развития орнамент достиг в средневековой Руси. Для русского орнамента характерны как геометрические и растительные формы, так и изображения птиц, зверей, фантастических животных и человеческих фигур. Наиболее ярко русский орнамент выражен в резьбе по дереву и вышивке. В плоском орнаменте одним из наиболее часто используемых мотивов является так называемая плетенка - различного вида переплетение полосок типа лент, ремней, стеблей цветов.

Трудно встретить человека, не любовавшегося орнаментами. Один из примеров, это обои, которыми оклеивают стены.

Орнамент -  украшение, узор, состоящий из ритмически организованных повторяющихся элементов. Для русского орнамента характерны как геометрические и растительные формы, так и изображения птиц, зверей, фантастических животных и человеческих фигур.

Орнамент служил не только украшением, но и заговором от злых сил природы, «оберегом». Поэтому и вышивались эти узоры, где одежда кончалась (т.е. в местах, где одежда касалась открытого тела) - у ворота, на   подоле, на манжетах. Кроме того, орнаментальные медальоны защищали плечи и колени.

Технику выполнения вышивки крестом часто называют «счетной», поскольку во время работы приходится точно рассчитывать количество стежков в рядах и цветных блоках.

В зависимости от сложности мотивов выделяется несколько групп геометрического орнамента коми: 
– орнамент из простых геометрических форм: точки, квадраты, прямоугольники, ромбы, крестики, диагональные линии, треугольники; 
 – орнамент в поперечную и продольную полоску, из комбинированных квадратов, прямоугольников и ступенчатых ромбов (характерен для вязания на спицах, резных изделий и меховой мозаики).

Коми - орнамент

Все красивое радует нас. Красота и гармония тесно связаны с симметрией, это подметили еще древние художники. Симметрия объекта всегда необходимы нашему зрительному восприятию для того, что бы мы могли считать этот объект красивым. Постепенно у нас формируется картина окружающего мира. Мы находим общее в различных предметах - симметрию. О симметрии можно говорить и словом поэзии и языком математики. С симметрией мы часто встречаемся в искусстве, архитектуре, технике, быту. В большинстве случаев симметричны узоры на коврах, тканях, обоях.

Так что же такое симметрия?

Мне бы хотелось ответить словами Г. Вейля.

"Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство:".

"Симметрия" - это слово пришло из греческого языка. Оно, как и слово "гармония", означает соразмерность.

Симметрия - это раздел математики, который изучает особую закономерность в расположении частей некоторого предмета.

Математически строгое представление о симметрии сформировалось в 19 веке. Немецкий математик Герман Вейля (1855-1955) дал современное трактование определения симметрии: симметричным называется такой объект, который можно как-то изменять, получая в результате то же, с чего начали. Симметрия бывает разной. Рассмотрим фигуру человека. Фигура человека симметрична относительно некоторой прямой. Если провести вертикальную прямую вдоль позвоночника и поставить зеркало вдоль прочерченной прямой, то отраженная в зеркальце половинка фигуры дополнит ее до целой (такой же, как исходная фигура).

Ассиметрия - нарушение, отсутствие симметрии.

Практическое задание:

№ 1.Постройте фигуру, симметричную относительно точки О

 

№ 2.Постройте фигуру, симметричную относительно прямой l.

 

№ 3 .Выполните поворот около точки О.

 

№ 4.Выполните параллельный перенос.

 

Орнамент как самостоятельное художественное произведение не существует. Орнамент всегда связан с формой, масштабом, материалом изделия, его практически назначением и художественно-образным смыслом. Орнамент способен выразить самые разнообразные ощущения: сдержанность и торжественность, легкость, изящество и плавность, внутреннее напряжение или спокойствие, свободное движение. Его эмоциональная выразительность бесконечна. В орнаменте всегда отражается характер и особенности культуры народа, создавшего его, а также эпоха, в которую он возник.

Орнамент имеет следующие особенности:

Состоит обычно из повторяющихся элементов-мотивов, которые являются основой орнамента. Определенное сочетание мотивов создает художественный образ.

Орнамент может быть повторяющимся и замкнутым (в круге, в квадрате).

Орнамент может быть многоцветным и одноцветным, выполнен на поверхности предмета выпукло, рельефно или, наоборот, углублен.

Виды орнаментов:

геометрический,

растительный,

зооморфный,

антропоморфный.

Искусство создания орнамента.

Построение орнамента на бесконечной полосе называется линейным, а на плоскости - сетчатым (или плоским) орнаментом.

Линейные орнаменты:

а) основной элемент орнамента переносится в определенном направлении (вдоль прямой) на одно и то же расстояние. В этом случае использован параллельный перенос; а прямая называется осью переноса. б) элемент орнамента симметричен другому элементу орнамента относительно прямой t, а затем эта элементарная ячейка (то есть фигура, за счет параллельного переноса которой получается весь орнамент) параллельно переносится вдоль прямой АВ, перпендикулярной t. в) элементарная ячейка (то есть фигура, за счет параллельного переноса которой получается весь орнамент) состоит из фигур симметричных друг другу относительно точки (то есть фигуры имеющие центр симметрии).

а) осевая симметрия относительно горизонтальной прямой, параллельный перенос вдоль этой прямой; б) осевая симметрия относительно вертикальной прямой, осевая симметрия относительно горизонтальной прямой, параллельный перенос; в) параллельный перенос с поворотом на 90°. Далее - параллельный перенос; г) осевая симметрия, параллельный перенос с поворотом 90°. Далее - параллельный перенос.

 развернуть таблицу

Сетчатые (плоские) орнаменты.

В основе любого орнамента на плоскости лежит одна из сеток, состоящих из одинаковых параллелограммов, прямоугольников, ромбов, квадратов, правильных треугольников.

 развернуть таблицу

Элементарная ячейка орнамента определяется ячейкой сетки: косой, прямоугольной, ромбической, квадратной или гексагональной. На любой сетке внутри одной ячейки основной элемент - мотив орнамента - может встретиться несколько раз или не повториться ни разу. Но чем сложнее устроена элементарная ячейка, тем оригинальнее и красивее выглядит орнамент. В таком орнаменте можно найти и поворотную, и переносную, и зеркальную симметрию.

Практическое задание.

Задание. Нарисуйте свой вариант геометрического или растительного орнамента в полосе для отделки изделий.

Занятие 14 – 15. Загадки и математика.

Загадки - это произведение фольклора, в котором предмет не назван, но даются его признаки, узнаваемые особенности, по которым можно найти отгадку.

Он давно знакомый мой. Сговорились две ноги

Каждый угол в нём прямой. Делать дуги и круги. (Циркуль)

Все четыре стороны

Одинаковой длины.

Вам его представить рад.

Как зовут его? (Квадрат).

Загадка 1.

Ответ: 92,5 кг.

Решение.
1. 196/2=98 (большой+пара белых+пара черных)
2. 264-98=166 (два больших)
3. 98-83=15 (пара белых+пара черных)
4. 15/2=7,5 (пара белый+черный)
5. 83+7,5=92,5

Загадка 2. Мальчик заплатил за бутылку с пробкой 11 рублей. Бутылка стоит на 10 рублей больше, чем пробка. Сколько стоит пробка?

Ответ: 50 коп.

Загадка 3. Девочке, у которой нет имени, задали вопрос сколько ей лет. Она ответила:

"В том году, когда я родилась, моему брату было четверть лет моего дяди. Сейчас моему брату исполнилась треть возраста моего отца. Мой возраст равен 1/4 текущего возраста моего дяди, а через 4 года мне исполнится 1/4 лет от будущего возраста моего отца".

Сколько лет девочке?

Ответ: девочке 9.6 лет, дяде 38.4, брату 16.8, отцу 50.4

Загадка 4. Сколько раз на протяжении суток минутная и часовая стрелки часов образуют прямой угол?

Решение. На протяжении суток минутная и часовая стрелки образуют прямой угол 44 раза. Есть два решения этой задачи.
1) Логическое. В сутки часовая стрелка делает 2 оборота, а минутная - 24 . Отсюда минутная стрелка обгоняет часовую 22 раза и каждый раз с часовой стрелкой образуется по два прямых угла, т. е. ответ - 44.
2) Математическое. За 1 час часовая стрелка описывает угол 30°, а за 1 мин. − угол 0,5°. Минутная стрелка за 1 мин. описывает угол 6°. Так как 90 : (6 − 0,5) = 16 (4 / 11), минутная и часовая стрелки образуют прямой угол в первый раз через 16 (4 / 11) мин. после того, как обе будут стоять на 12. Так как n × 16 (4/11) = 24 × 60, мы получаем n = 88 (в это число входят углы в 0°, 90°, 180° і 270°, образованные минутной и часовой стрелками).

Загадка 5

Ответ: 39

Загадка 6.

На пиратском корабле несколько кошек, немного матросов, кок и одноногий капитан Сильвер. У них всех, вместе взятых, 15 голов и 41 нога. Сколько на корабле было кошек?

Ответ: Шесть кошек. Капитан - одноногий, следовательно на 14 голов приходится 40 ног. Лишних ног (если у всех по две) 40 - 28 = 12. Надо добавить по 2 ноги на каждую кошку. Итого получается: 1 капитан, 7 матросов, 6 кошек и кок.

Загадка 7.

Сказочному гному еженощно нужна новая свеча, которой он светит себе в дороге, ходя по городу. Он может сделать 1 новую свечу из 5 свечных огарков. Если у него наберется 25 огарков, то на сколько ночей ему хватит запаса новых свечей?
Ответ: На 6 ночей. Он сможет сделать 5 новых свеч из 25 огарков, а когда они сгорят, он может сделать шестую из тех 5 огарков, что от них останутся.

Загадка 8.

Дано денег - Один рубль. На эти деньги нужно купить ровно 100 яиц - гусиных, утиных, куриных:
- гусиные - по 5 коп./шт;
- утиные - по 3 коп./шт;
- куриные - 1 коп./десяток.
На рубль нужно купить нужно 100 яиц, без сдачи.
Ответ: Гусиных - 16, утиных – 4, куриных - 80.

Загадка 9.

Василию, Петру, Семену и их женам Наталье, Ирине, Анне вместе 151 год. Каждый муж старше за свою жену на 5 лет. Василий на 1 год старше Ирины. Наталье и Василию вместе 48 лет, Семену и Наталье вместе 52 года. Кто на ком женат, и сколько кому лет? (Возраст должен быть выражен в целых числах).

Ответ: Василий (26) - Анна (21); Петр (27) - Наталья (22); Семен (30) - Ирина (25)

Загадка 10.
На столе лежит десять пронумерованных шляп. В каждой шляпе лежит по десять золотых монет. В одной из шляп фальшивые монеты. Настоящая монета весит 10 граммов, а поддельная только 9. В помощь даны весы со шкалой в граммах. Как определить в которой из шляп находятся фальшивые монеты, используя весы только для одного взвешивания? Весы могут взвешивать не больше 750 грамм.

Ответ: Из первой шляпы берем одну монету, из второго две, из третьего три и так далее, кладем все эти монеты на весы. Если бы все монеты были настоящими, то вес был бы: 10*(1+2+3+4+5+6+7+8+9+10). Вместе: 550 грамм. Но несколько монет являются фальшивыми, а сколько - легко узнать. Достаточно из 550 отнять тот вес, что мы получили, и мы увидим «погрешность», равную количеству фальшивых монет. Количество монет укажет на шляпу.

Загадка 11.

У Змея Горыныча 3 головы и 3 хвоста. Одним ударом меча-кладенца Илья Муромец может отрубить одну или две головы или же один или два хвоста.

Если он отрубит один хвост, то вырастут 2 новых хвоста.
Если он отрубит 2 хвоста, то отрастет 1 голова.
Если отрубить одну голову, то вырастет одна новая голова.
Лишь в том случае, если отрубить две головы, то ничего не вырастет.

Змей погибает только в том случае, если у него не остается ни одной головы и ни одного хвоста, причем в этот момент у него ничего не должно отрастать. Может ли Илья победить, если у меча-кладенца есть заряд всего на девять ударов?

Ответ: Может. Сначала нужно отрубить 3 раза по одному хвосту, затем 3 раза по два хвоста, и наконец 3 раза по две головы.

Загадка 12.

Проехав треть пути, пассажир скорого поезда наконец заснул. Когда он проснулся, до станции назначения оставалось проехать половину того расстояния, что отделяло его от станции назначения, когда он заснул.
Какую часть пути проехал поезд, пока пассажир спал?

Ответ: Так как (1/2) × (2/3) = 1/3, пассажир проспал 1/3 пути.

Загадка 13.

Это старинная народная задача. Крестьянка пришла на базар продавать яйца. Первая покупательница купила у нее половину всех яиц и еще пол-яйца. Вторая покупательница приобрела половину оставшихся яиц и еще пол-яйца. Третья купила всего одно яйцо. После этого у крестьянки не осталось ничего. Сколько яиц она принесла на базар?

Ответ: Задачу решают с конца. После того как вторая покупательница приобрела половину оставшихся яиц и еще пол-яйца, у крестьянки осталось только одно яйцо. Значит, полтора яйца составляют вторую половину того, что осталось после первой продажи. Ясно, что полный остаток составляет три яйца. Прибавив пол-яйца, получим половину того, что имелось у крестьянки первоначально. Итак, число яиц, принесенных ею на базар, семь.

Загадка 14.

Для взвешивания товара продавец пользуется чашечными весами и четырьмя гирями общим весом 40 кг. Причем, используя разные комбинации гирь, можно взвесить любой груз, масса которого выражается целым числом килограммов (от 1 до 40 кг). Сколько весит каждая гиря?

Ответ: Гири весом в 27, 9, 3 и 1 кг.

Занятие 16. Математика в скороговорках

Скороговорка – это интересная фраза с подбором звуков, трудных для произношения, которая быстро и четко проговаривается.

Скороговорки - шуточный жанр народного творчества, фраза, построенная на сочетании звуков, которые затрудняют быстрое произношение слов.
Существует огромное количество различных скороговорок. Их можно поделить на простые и сложные. Простые предназначены для усовершенствования выговаривания только одного звука. Намного сложнее научится проговаривать сочетание трудных фонем либо различать близкие по значению звуки. Тут на помощь приходят сложные скороговорки. Они также делятся на короткие, состоящие из одного слова и длинные – складываются из нескольких слов, бессюжетные и с сюжетной линией, написаны в прозаичной форме или стихом. Часто встречается деление по возрастной категории – детские и взрослые.

Значение скороговорок переоценить сложно. Они помогают развивать хорошую дикцию, улучшают память, расширяют словарный запас, развивают слуховое внимание.

Скороговорки – это еще и забава. Ведь чтобы правильно ее выговорить нужно повторить несколько раз иногда совершая ошибки. Хорошо посмеяться вместе, над словами, которые не получаются. Но здесь скрывается еще один смысл. Ребенок учится воспринимать маленькие неудачи, в виде корявых слов. Он видит, что и старшие делают похожие ошибки. Такая совместная работа научит детей не так болезненно воспринимать промахи в будущем.

Красивая дикция – украшение человека. Для ее усовершенствования хорошо подойдут скороговорки. Тем более что изучать их можно на протяжении всей жизни.

 Скороговорки по математике

Три сороки, три трещотки потеряли по три щетки: три - сегодня, три - вчера, три - еще позавчера.

Четыре черненьких чумазеньких чертенка чертили черными чернилами чертеж чрезвычайно чисто.

Во дворе четыре Сашки на траве играли в шашки.

У четырех черепашек по четыре черепашонка.

Полчетверта четверика гороху, без червоточинки.

Опять пять ребят нашли у пенька пять опят.

Шесть мышат в камыше шуршат.  

Саша шустро сушит сушки,
Саша высушил штук шесть.
И спешат к нему старушки сушек
Сашиных поесть.

На семеро саней по семеро в сани уселись сами.

 

Cкороговорки с числами и цифрами

Шестнадцать шли мышей,
нашли по сорок грошей,
две мыши поплоше
нашли по две гроши.

Тридцать три корабля лавировали, лавировали да не вылавировали.

 

Скороговорки с именами числительными

 

 Съел молодец 33 пирога с пирогом, да все с творогом.

Как на горке на пригорке жили тридцать три Егорки: раз Егорка, два Егорка, три Егорка…

Полпогреба репы, полколпака гороху.

Головоломка: С помощью цифр от 0 до 9 записана скороговорка. Каждой цифре соответствует одна буква, причем буквы пронумерованы в алфавитном порядке (е=ё).

940 7090 65 95771 2 757040 78938

Решение: 0-А, 1-Е, 2-И, 3-К, 4-Л, 5-О, 6-П, 7-С, 8-У, 9-Ш

Шла Саша по шоссе и сосала сушку.

Занятие 17. Математические формулы, теоремы и правила в частушках.

Частушка – короткая (обычно 4-строчная), исполняющаяся в быстром темпе, рифмованная припевка русского народного словесно-музыкального творчества. Первоначально частушку не признавали за художественный жанр народного творчества, считали, что она испортит и погубит народную песню. В XX веке острота и своеобразие частушечных мелодий привлекли внимание композиторов. Создано немало разнообразных авторских произведений в этом жанре. Сейчас частушка живет полноценной, творческой жизнью, занимает немалое место в русской национальной песенной культуре.  

Типы частушек.

Лирические частушки (припевки) — четырехстрочная частушка на разные темы.

Плясовые — четырехстрочные припевки, они отличаются от лирических особым ритмом, удобным для сопровождения плясок, строчки короче, чем в лирической частушке. К ним относятся частушки типа «Яблочко», которые появились в начале XX века на Украине, как любовные. В 1917—1920 годы эти частушки обрели новую тему, став социально-политическими.

Страдания — как правило, двухстрочные частушки о любви — поются медленно, протяжно. Их пели на Волге и в средней полосе России. На Севере России, Урале, Сибири они не были известны.

Частушки, названные по зачину — «Семеновна». Это двухстрочные частушки с особым заунывным ритмом. Появились в 30-е гг. XX века.

Существует множество частушечных напевов. Часто текст частушки распевают на один и тот же знакомый мотив.

В математике задачи

Словно в жизни неудачи

И скажу я вам ребята.

Как решать их непонятно.

Математика наука

Всех наук - нам говорят,

А ведь в жизни нам науки

Никогда не повредят.

Биссектриса это крыса,

Только я не поняла

Для чего же эта крыса

Делит угол пополам.

Пифагоровы штаны

Во все стороны равны,

Их не пробуй надевать

Ноги не куда девать.

Я примерный ученик

Всю таблицу знаю

5*5=25,

6*6 –не знаю.

Математик Пифагор

Супер джинсы изобрел

Говорят его штаны

Во все стороны равны.

Мы с решебника списали,

Думали все правильно,

А на алгебру пришли -

Двойку нам поставили.

На уроке я была

Алгебру учила

На контрольной отсидела

Пару получила.

На компьютере играли

Мы на информатике,

Только 2 получили

Мы на математике.

Геометрию мы любим,

Решаем мы ее всегда,

Но хорошие оценки

Получаем иногда.

Теоремы, теоремы

До чего вы довели

Иксы, минусы, задачи

Вы с ума меня свели.

Уравненья я люблю

В классе отвечаю

А когда домой приду

Тут же забываю.

Математику люблю

С калькулятором дружу

На контрольной я сижу,

Калькулятор достаю.

У меня в задачнике

Трудные задачки

Я всегда смогу решить

С помощью подсказки.

Мне казалось всегда,

Геометрия сложна

Только пару получила

Весь учебник изучила.

Я не знала никогда,

Теорему всю угла

Геометрию учу,

Любой угол начерчу.

Мы задачи все решаем,

И пятерки получаем

Но бывает иногда,

Получаем цифру 2.

Уравнение решать -

Дело непростое.

Плюс на минус поменять -

Правило такое.

Вертикальные углы

Говорят, что все равны

Только я не верю вам

Транспортиром измерю сам.

Я на алгебре сижу,

Слушаю внимательно.

Задачу сложную свою -

Решу я окончательно.

Уравнения, уравнения

До чего вы довели

Иксы, минусы, деление -

Вы меня с ума свели.

Я контрольную писала

Получила двойку,

Порешаю я сегодня

Получу пятерку.

Днем и ночью я не сплю

Геометрию учу,

А как выйду я к доске

Станет мне не по себе.

Уравнения я знаю

И решаю их на 5.

Только я не понимаю,

Где прибавить, где отнять.

Мы зачет вчера писали,

Очень сильно мы устали,

А вот Вадя не устал,

Взял зачет, да и списал.

Геометрию учу,

Все я понимаю.

Как домашнюю пишу,

Сразу забываю.

Геометрию учила

И пятерку получила

А на физику пришла,

Поседела и ушла.

Чтобы скорость рассчитать -

Надо быстро рассуждать.

Путь на время подели

И к ответу подгони.

Синус, косинус, квадрат

Как Семен сегодня рад.

Ведь задачу он решил

И пятерку получил.

Извлекали мы квадрат

Из числа обычного,

Только вышел результат

Весьма неприличный.

Математику я знаю,

Информатику учу.

Я пятерки получаю,

В ВУЗ, наверно, попаду.

Полюбила программиста,

Голова из трех частей -

Монитор, клавиатура,

Мышка с ковриком при ней.

Геометрия наука -

Очень сложная друзья.

Вот поэтому ребята

Шпоры делать здесь нельзя.

Чтоб задачи сложные с лёту все решить,

Алгебру – науку нужно изучить,

Алгебру – науку нужно изучить.

И тогда пятёрочку сможем получить.

Занятие 18 - 19. Пословицы и поговорки в графиках и диаграммах

Пословицы – это краткие изречения, в которых выражены жизненные наблюдения и правила житейской мудрости.

Чтобы научиться трудолюбию, нужно три года.

Чтобы научиться лени – только три дня.

Не строй семь церквей, а пристрой семь детей (сирот).

Лучше один раз увидеть, чем сто раз услышать.

Поговорки – это меткое народное выражение, краткое по форме, острое по мысли.

Плакать в три ручья.

От горшка три вершка.

Лук от семи недуг.

Задание 1

6

5

4

3

2

1

Ответы:

1.Любишь с горочки кататься – люби и саночки возить.

2.Тише едешь, дальше будешь.

3.Как аукнется, так и откликнется.

4.Чем больше народа в помещении, тем меньше кислорода.

5.Чем дальше в лес, тем больше дров.

6. Повторенье – мать ученья.

Задание 2

Нарисовать диаграмму к пословице «В гостях хорошо, а дома лучше».

Задание 3.

Занятие 20. Пестушки. Дразнилки и считалки с числами.

Пестушки получили своё название от слова «пестовать», что значит нянчить, оберегать, успокаивать. Это короткие стихотворные приговоры, которыми сопровождаются движения младенца с первых дней его жизни.

Идут четыре брата

Навстречу старшему.

- Здравствуй, большак! – говорят.

- Здорово, Васька-указка,

Мишка-середка,

Гришка-сиротка

Да крошка Тимошка.

Три-та, та, три-та, та!

Вышла кошка за кота.

За Кота Котовича,

За Петра Петровича.

Раз ку-ку, 
Два ку-ку, 
Провалился кот в муку. 
Нос в муке, 
Хвост в муке, 
Ушки в кислом молоке. 

Дразнилки отражают негативные моменты в восприятии детьми окружающей действительности. Дразнилка предназначена для того, чтобы поставить обидчика на место, высказать своё отношение к неприятным отклонениям в поведении, в привычках, во внешнем виде.

1. Обманули дурака

На четыре кулака,

На пятое - стуло,

Чтоб тебя раздуло!

На шестое – колесо,

Чтоб тебя разнесло.

2. Рёва – корова,

Дай молока.

Сколько стоит?

Три пятака.

3. Робин Бобин Барабек
К. Чуковский

Робин Бобин Барабек
Скушал сорок человек,
И корову, и быка,
И кривого мясника,
И телегу, и дугу,
И метлу, и кочергу,
Скушал церковь, скушал дом,
И кузницу с кузнецом,
А потом и говорит:
«У меня живот болит!»

Считалки – ритмично произносимый стишок, в результате которого определяются места участников в детских играх.

1.«Раз, два, три, четыре, 3. Сидели два медведя

пять, шесть, семь, На липовом суку,

восемь, девять, десять. Один читал газету,

Выплывает белый месяц. Другой месил муку

Кто до месяца дойдёт, Раз ку-ку, два ку-ку.

Тот и прятаться пойдёт». Оба шлёпнулись в муку.

2. Чищу овощи для щей.

Сколько нужно овощей?

Три картошки, две моркови,

Лука полторы головки,

Да петрушки корешок,

Да капустный кочешок.

Потеснись-ка ты капуста,

От тебя в кастрюле густо.

Раз, два, три, огонь зажжён,

Кочерыжка, выйди вон!

Занятие 21- 22. Математический фольклор народов мира 2 часа

Наряду с такими видами фольклорного творчества, как загадки, сказки, легенды, песни, прибаутки, пословицы и поговорки, существует еще один, не менее интересный вид народного творчества - занимательные математические задачи, относящиеся к математическому фольклору. В этом виде творчества, передаваемом устно в течение многих лет от одного поколения к другому, можно увидеть всю красоту математических закономерностей, описывающих многие процессы и явления окружающей действительности.

Как и в других видах народного творчества, фольклорные математические задачи не имеют авторов. Они и забавляют, и проверяют способности людей к остроумию, сообразительности, логичным рассуждениям. Условия и решения занимательных задач вызывают не меньший интерес, чем увлекательные сказки и легенды, острометные пословицы и поговорки.

Рассмотрим некоторые из них.

Болгарская задача

Пастух пас стадо из 100 голов. За это ему платили 100 лв. (1лв. - лев - болгарская денежная монета). За каждого вола он получал 10 лв., за каждую корову - по 5 лв., а за теленка - по 50 ст. (1 ст. - стотинка - денежная единица в Болгарии, 1 лв. = 100 ст. 50 ст. = 0,5 лв.). Сколько в стаде волов, коров и телят?

Ответ: 1 вол, 9 коров и 90 телят в стаде.

Русская задача

Царь ему разрешил. Пошел крестьянин к саду и видит: весь сад огорожен тройным забором. В каждом заборе есть только одни ворота, около каждых ворот стоит один сторож.

Подошел крестьянин к первому сторожу и сказал: «Царь разрешил мне взять одно яблоко из сада».

«Возьми, но при выходе должен будешь выдать мне половину тех яблок, что возьмешь, и еще одно», - сказал сторож.

Это же сказали ему второй и третий сторожа, которые охраняли другие ворота.

Ответ: 22 яблока.

Бразильская задача

Каждое утро Рейнальдо выпивает чашку крепкого кофе, которая содержит определенную дозу кофеина. Однажды он приготовил кофе из партии зерен, из которых уже было извлечено 97% кофеина. Сколько чашек такого кофе нужно выпить, чтобы в них содержалось столько кофеина, сколько содержалось в одной чашке крепкого кофе?

Решение:

Нужно выпить 33 чашки кофе. Поскольку в данной партии оставлено всего 3% кофеина, то в 100 чашках его будет содержаться столько же, сколько в трех чашках обычного кофе. А если 100 разделить на 3, то как раз и получится 33, приближенно 33 чашки кофе.

Ответ: 33

Задача из Древней Греции.

Обратились к Хроносу – богу времени:

«Скажи, о Хронос, предвестник будущего, какая часть дня прошла?»

Последовал ответ:

«Осталось ещё удвоенное двух третьих времени, которое прошло».

В каком часу был этот разговор, если считать, что день начинается в 6 часов утра, а длится 12 часов.

Ответ: в 11 часов 8 минут.

Cтаринная арабская загадка

Охотник встретил двух пастухов, у одного из которых было три куска хлеба, а у второго - пять. Все куски были одного размера.

Трое мужчин разделили весь хлеб поровну. После еды, охотник дал пастухам восемь монет на двоих. Как пастухи должны разделить эти деньги?

Ответ:Первый должен получить одну монету, а второй - семь.

Задача из Египта

Каждый из семи человек имеет по семь кошек. Каждая кошка съедает по семь мышек, каждая мышка за одно лето может уничтожить семь ячменных колосков. Из зерен одного колоска может вырасти семь горстей ячменного зерна. Сколько зерен ежегодно спасается благодаря мышкам?

Ответ:16807 горстей

Индийская задача

Из четырех посетителей храма второй дал в два раза больше монет, чем первый, третий – в три раза больше монет, чем второй, а четвертый – в четыре раза больше, чем третий. Всего было дано 132 монеты. Сколько дал первый?

Ответ: 4 монеты

Задача из Франции

Три брата хотели купить новый дом, который стоил 26 тысяч франков. Они условились, что первый даст половину цены, второй – одну четвертую. Сколько заплатил каждый из братьев?

Ответ: 12000 франков – первый, 8000 франков – второй, 6000 франков – третий

Греческая задача

Идут нагруженные осел и мул. Осел жалуется на непосильную ношу, мул отвечает: «Что ты жалуешься? Если я возьму один твой мешок, то моя ноша станет в два раза тяжелее. А если ты возьмешь один мой – то наши будут равны. По сколько мешков несли осел и мул?

Ответ: по 5 и 7 мешков

Немецкая задача

За какое время лев, волк и собака могут съесть три овцы, если лев может съесть овцу за один час, волк – за три часа, а собака съедает овцу за шесть часов?

Ответ: за 2 часа

Задача из Австралии

Скотовод завещал своим сыновьям разделить стадо овец: первый сын получит на двадцать процентов больше второго и на двадцать пять процентов больше третьего. Часть второго сына – 3600 овец. Сколько овец получит третий брат?

Ответ: 3456 овец

Задача из России

Крестьянка несла на базар корзину яблок. Первому покупателю она продала ½ всех яблок и еще ½ яблока, второму – 12 от яблок оставшихся и еще ½ яблока, третьему – половину от остатка и ½ от яблока и т.д. Когда шестой купил ½ ½ оставшихся и еще ½ яблока, то в корзине ничего не осталось. Сколько яблок было у крестьянки, если все покупатели приобрели целое число яблок?

Ответ: 63 яблока

Занятие 23-24. Военно – патриотические задачи

С каждым годом становится все меньше живых свидетелей кровавых событий Великой Отечественной войны. Современные дети не представляют себе, что пережил наш народ в тяжелые военные  годы. Мы не вправе забывать об этом, и должны быть патриотами своей Родины.

В октябре 1941 года враг совершил на Москву 31 налет. В этих налетах участвовало 2000 немецких самолетов, из них было сбито 278. К городу прорвалось только 72 самолета. Сколько вражеских самолетов не сумели прорваться к Москве? 

12 июня 1812г. французские войска перешли границу России, 1 января 1813 г. побежденные французы оставили территорию России. Сколько дней длилась война с Наполеоном на территории России?

Под Бородино сражалось 135 тысяч французских и 120 тысяч русских воинов.  Погибло 58,5тысяч французов и 45,6 тысяч русских. Сколько процентов французов и сколько процентов русских осталось в живых? Ответ округлите до целых.

Во время наступательной операции бригада солдат разделилась на три батальона: первый батальон составлял 450 бойцов, другой на 130 бойцов меньше, а в третьем батальоне солдат было в 2 раза меньше, чем в первом и во втором вместе взятых. Какова общая численность бригады солдат?

В Великую Отечественную войну на одном из заводов за несколько часов было выпущено 160 винтовок, среди которых 16 – с дефектами. Найдите вероятность того, что солдату попадётся качественная винтовка.  

Танк Т-34, выехав из Курска к Прохоровке со скоростью 50 км/ч, добрался до места сражения за 2,5 часа. За какое время доберется до Прохоровки танк ИС-76, скорость которого равна 31,25 км/ч, если, встретив сопротивление на полпути к цели, ему пришлось возвращаться к Курску и начинать движение заново? (Считать, что на всем пути, скорость танка была постоянной)

В начале войны бюджет одной из противоборствующих сторон составлял один миллиард долларов. Сколько оставалось средств в бюджете, если в ходе войны страна выделила 25% средств из бюджета на покупку танков T-275 "Рогатка", 30% на покупку противотанковых ракет "Метис" и 50% оставшихся денег на покупку самоходных гаубиц 2С1 "Гвоздика"?

Узнать, сколько дней продолжалась война, поможет вам удивительный квадрат. Выберите из каждой строки и каждого столбца по одному числу, найдите сумму выбранных четырех чисел, и вы получите ответ на вопрос.

413	218	474	567
569	374	630	979
195	0	256	349
221	26	282	375

На момент вторжения немецко-фашистских агрессоров враг превосходил наши войска по личному составу в 1.8 раза, по тяжелым и средним танкам в 1.5 раза, по самолетам новых типов в 3.2 раза, по орудиям и минометам в 1.25 раза. Каково было вооружение захватчиков, если в войсках, прикрывавших Западные границы СССР, было 2.9 млн. человек, 1540 самолетов нового типа, 34695 орудий и минометов, 1800 тяжелых и средних танков?

Максимальная скорость танка Т-34 образца 1940 года 51,2 км/ч. Какое расстояние способен преодолеть танк по открытой местности в марше за неделю?

В октябре в район Сталинграда было подано 33236 вагонов с личным составом и боевой техникой, а в ноябре 41461 вагонов. Сколько всего вагонов было поставлено в район боевых действий?

С 1 по 19 ноября через реку,  покрытую льдом. Было перевезено 160 тыс. солдат, 10 тыс. лошадей, 430 танков, 600 орудий, 14 тыс. автомашин, 7 тыс. боеприпасов. Оформить данные переброски войск в таблицу.

У Германии было 5тысяч самолетов, а у России 15 тысяч. Германия уничтожила у России 20%самолетов, а Россия у Германии 60%. сколько у каждой страны осталось самолетов?

Война длилась 547 дней, но известно, что за всю войну 136дня и 35 минут военных действий не велось. сколько всего велось военных действий в минутах?

Занятие 25 – 27. Краеведческий фольклор

НАШ ДРЕВНИЙ ГОРОД

Что на славной реке Вологде,

Во Насоне было городе,

Где доселе было – Грозный царь

Основать хотел престольный град

Для свово ли для величества

И для царского могущества;

Укрепил стеной град каменной

Со высокими со башнями,

С неприступными бойницами;

Посреди града он церковь склал,

Церковь лепую соборную... (Народная песня)

Русский Север – край широких рек, светлых озер, дремучих лесов, страна дивных деревянных построек и монументальных каменных ансамблей. Особое место в истории Севера и его художественной культуры принадлежит Вологде. Здесь сначала в церквях и монастырях, а затем в музеях образовались прекрасные коллекции произведений искусства как северного, так и столичного происхождения. Вологда – город-музей. Она интересна для нас не только памятниками искусства и зодчества, но и своим неповторимым обликом.

Вологда. Старинный русский город, возникший в краю дремучих лесов, тихих бескрайних озер и чистых прозрачных рек. По ним пробирались в своих ладьях-ушкуях новгородские ушкуйники, отвоевывая у местного населения все новые и новые земли. С приходом новгородцев на берегах тех же рек и озер стали появляться небольшие церковки, часовенки, а затем монастыри и крепости. Так возникло на правом высоком берегу реки Вологды небольшое поселение, превратившееся затем в город Вологду.

Задание 1. Если вы правильно решите примеры, то узнаете примерную дату основания Вологды. В-1. 104 · 12 + 493 : 17 – 130 =

В-2. 2346 : (209 – 186) · 8 + 331=

В-3. 6720 : 12 · 7 – 2773 =

В-4. (1519 + 1922) : (342 : 114) =

Задание 2. Рим был основан в 753 году, а Вологда на 1394 года позже. В каком году основана Вологда?

Задание 3. Происхождение слова Вологда объясняют различно. Одни считают, что слово Вологда произошло от финского слова «Волокъва», другие – от слова «Волокъ».

Выполните устно задания и вы узнаете, значение этих слов в переводе на русский язык.

В-1 В- 2. Ключ: 1. 100 : 2 = 1. 35 · 2 = и => 51

2. 24 · 3 = 2. (333 + 93) – 33 = ш => 3

3. 206 + 17 = 3. 83 – 33 = л => 50

4. 96 – 54 = 4. 271 + 45 = с => 223

5. 123 + 15 – 23 = 5. 600 : 200 = а => 115

6. 13 · 11 = 6. 131 · 3 = о => 393

7. (207 + 94) – 7 = 7. 255 : 5 = ь => 245

8. 100 – 28 = 8. 27 + 23 = н => 42

9. 666 : 333 = 9. 144 : 2 = я => 143

10. 290 – 175 = 10. 300 – 77 = р => 294

е => 72

к => 2

Софийский собор – памятник истории культуры

Центральное сооружение на территории Вологодской крепости – Софийский собор, главная святыня Вологды. Это первый каменный храм города. Он был построен в 1568–1570 годах, но его освещение произошло в 1588 году, так как при осмотре Иваном IV готового здания «нечто отторгнувся от свода и, над, государю повреди главу». Царь разгневался и даже приказал разрушить собор, но его упросили не приводить намерения в исполнение, и царь уехал из Вологды. С юго-западной стороны Софийского собора возвышается стройная колокольня. Основу ее составляет древняя колокольня, построенная между 1654 и 1658 годами. В 1869–1870 годах колокольня была перестроена. На колокольне сохранился ряд древних колоколов XVII века: Большой или праздничный (1687 год), Архангельский (1689 год), Большая лебедь (1682 год), Часовой (1627 год), Великопостный или Водовоз (1643 год) и другие. Колокольня примыкает к Архиерейскому дому. До XVII века Архиерейский дом не имел каменных сооружений. Высокие каменные стены с башнями были возведены в 1671–1675 годах. Стены и башни не представляют большой ценности, но постройки внутри стен очень интересны. Например, казенный приказ, построенный в 1659 году. Это здание с тяжелыми дверями, железными засовами и темными чуланами.

Задание 4.

Выпишите номера примеров, в которых допущены ошибки, и вы узнаете год, когда был построен Софийский собор.

1) 100 – 25 = 65 ; 2) 45 · 11 = 495; 3) 933 : 3 = 311;

4) 873 + 22 + 27 = 922; 5) 38 · 5 = 180; 6) 1095 : 5 = 218;

7) 897 – 252 = 645; 8) (763 + 54 ) – 63 = 750; 9) 653 – 544 = 109.

Задание 5.

В 1568 году Иван Грозный начал строить кафедральный собор во имя Софии Премудрости. Сколько лет стоит замечательный памятник архитектуры и живописи – величественный собор Софии?

Задание 6.

Найдите годы росписи Софийского собора, если известно, что сумма их цифр равна 2374, а вторая дата больше первой на 2.

Задание 7. Решите уравнение и вы узнаете площадь фресок Софийского собора.

(х – 3745) : 5 = 251 24 · ( х : 25 ) = 4800

Задание 8. Напротив Софийского собора находился двор архиепископа, окруженный забором: 70 сажень вдоль и 60 сажень поперек. Найдите площадь двора в саженях и квадратных километрах, зная, что одна сажень примерно равна 2 метрам 13 сантиметрам.

Задание 9. В 1642 году была срублена деревянная колокольня Софийского собора. Мастер Карп Евтихиев отлил для нее большой и малый колокол. Вес большого колокола был на 103 пуда тяжелее малого. Найти вес каждого колокола, если общий вес двух колоколов – 141 пуд. Выразить вес каждого колокола в килограммах, зная, что 1 пуд равен 16 килограммам.

Задание 10. В 1654–1659 годах в Вологде построили каменную колокольню. Крестьяне села Вятского изготовили для колокольни за 3 года 134 150 штук кирпича. Во второй год кирпича изготовили в 3 раза больше, чем в первый, а в третий – на 2102 штуки больше, чем во второй. Сколько кирпича изготовляли каждый год?

Задание 11. Продолжите ряд и вы узнаете, сколько денег царь Алексей Михайлович пожертвовал на постройку каменной восьмишатровой колокольни, построенной в 1654–1659 годах? 450, 460, 480, 510, 550, 600, ...

Задание 12. Площадь чугунного пола Софийского собора – 700 квадратных метров, а ширина 25 метров. Найдите длину пола и его периметр. Сколько штук бордюра длиной 2 метра потребуется для работы.

Задание 13. Первая деревянная колокольня Софийского собора была срублена через 475 лет после основания Вологды. Каменная колокольня была построена еще через 32 года. Когда была построена каменная колокольня?

Задание 14. Первая каменная колокольня Софийского собора на 22 метра ниже высоты средней главы Софийского собора. Найти высоту средней главы Софийского собора, если сумма этих величин – 98 метров.

Задание 15. В 1870 году колокольня была перестроена. Выполните задания и вы узнаете: а) высоту колокольни; б) высоту смотровой площадки; в) количество ступеней на колокольне; г) вес самого большого колокола; д) количество колоколов.

Решить уравнение: а) 2х – 2 = 155;

б) а · а + 1 = 4226,

какое из чисел является корнем уравнения: 55 или 65;

в) (у – 300) · 5 = 0;

г) 3 · (2х + 1) = 153;

д) х · х = 1600.

Задание 16.По данным летописи в 1780 году в Вологде было деревянных церквей в 4 раза больше, чем монастырей, а каменных церквей в 4 раза больше, чем деревянных церквей и монастырей вместе. Общее количество церквей и монастырей в городе было 50. Сколько каменных церквей было в Вологде в 1780 году?

Задание 17. Какую площадь имел город в XVIII веке, если он тянулся в длину с Севера на Юг на 5 верст, а в ширину с Запада на Восток – на 3 версты. Выразите длину и ширину в километрах и найдите площадь в квадратных километрах, если 1 верста примерно равна 1 километру 70 метрам.

Задание 18.

19 ноября 1700 года русская армия потерпела под Нарвой поражение и потеряла все пушки. Исключите лишнюю дробь, умножьте ее на 10 000 и вы узнаете, сколько пудов колокольной меди было отправлено из Вологды для литья новых пушек. 0,27; 0,81; 0,1; 0,54; 0,9; 0,99.

Задание 19. Петровская эпоха внесла много существенных перемен в жизнь северного края. Строительство военных кораблей в Архангельске и Петербурге потребовало притока в эти города рабочей силы. Сколько плотников с семьями в 1721 году, «годных для судовой работы», необходимо было отправить из Вологды в эти города?

0,25 · 16  ? + 2,93 : 2,31  ? · 1,45 – 2,35  ? + 2,32  ? · 100  ?

В 1797 году Вологодская губерния имела десять уездов: Вологодский, Велико-Устюгский, Вельский, Грязовецкий, Кадниковский, Никольский, Сольвычегодский, Тотемский, Усть-Сысольский, Яренский. В1833 году в ней насчитывалось 645 тысяч жителей. Население занималось хлебопашеством, скотоводством, охотой. Сеяли рожь, пшеницу, ячмень, овес, лен, гречиху, горох. Сажали овощи, картофель. Промышляли дичь: медведей, лисиц, волков, бобров, выдр, белок, барсуков. В первой половине XIX века в губернии было 114 фабрик и заводов. Из них: 6 винокуренных, 9 солодовенных, 10 красильных, 2 канатных, 6 прядильных, 2 бумажных, 1 набойный, 2 лесопильных, 1 сахарный, 20 кожевенных, 16 свечных, 3 чугунных, 3 солеваренных, 33 кирпичных. В Вологде было 2 завода по литью колоколов. В 1780 году был составлен план города Вологды. Улицы города должны были образовывать четкую прямоугольную систему. Центральная улица Пятницкого замыкалась Софийским собором. Ширина жилых улиц составляла 27–29 метров. 17 мая 1782 года землемер Бровцин составил «геометрический специальный план города Вологды». По этому плану Вологда занимала 756,15 гектаров. Большие столбовые дороги – 25,14 га, проселочные – 7,19 га, чистых болот полгектара, реки и ручьи занимали 78,48 га. Под пашней значится 96,78 га, под покосом – 680 га, под лесом – 710,16 га. Всей земли города в окружной меже – 2413,83 га.

Задание 20. В 1820 году Вологодская губерния имела протяженность с юго-запада на северо-восток до 1280 километров, а ее протяженность с севера на юг составляла 48% этой величины. Найдите площадь Вологодской губернии.

Задание 21. В 1833 году Вологодская губерния насчитывала 645 000 жителей. Хозяйственные крестьяне составляли 27,3%, удельные – 14%, помещичьи – 4%, а остальные – свободные хлебопашцы. Сколько хозяйственных, удельных, помещичьих крестьян и свободных хлебопашцев насчитывала Вологодская губерния в 1833 году.

Задание 22. В первой половине XIX века в Вологодской губернии было 114 фабрик и заводов. Из них: 2 бумажные фабрики, 3 солеваренных завода, 33 кирпичных завода. Сколько процентов составляют бумажные фабрики, солеваренные и кирпичные заводы?

Задача 23. По специальному «геометрическому плану», составленному в 1782 году, Вологда занимала 756,15 га. Столбовые и проселочные дороги составляли 4,27%. Найдите площадь дорог.

Занятие 28. Сказки учителя. «Как отрицательные числа появились на числовой прямой?»

В математическом царстве, числовом государстве жили-были натуральные числа и ноль. Правил царством мудрый ноль. Жили числа дружно. Вместе строили дома, дом от дома на одинаковом расстоянии. Так получилась целая улица. В начале улицы жил ноль, в следующем доме единица, затем двойка и так далее. Улица убегала в туманную даль, потому что чисел в числовом царстве было бесконечно много.

И вот однажды появились в царстве непрошенные гости. На вид такие же числа, но вели себя как отрицательные личности. Устраивали драки, ссорились, пытались выселить натуральные числа из их домиков. Пошли натуральные числа к мудрому нолю и спросили: «Что делать?» Ноль рассудил так: «Пусть живут отрицательные числа в числовом царстве, но дома себе саами построят и продолжат улицу влево от ноля».

Сказано-сделано. В миг слева от дома ноля выросли новенькие домики, и улица скрылась в бесконечности. Все успокоились. Но не на долго. Теперь стали путаться почтальоны. Придет письмо числу 5, а почтальон его в дом отрицательного числа 5 отнесет и наоборот. Снова ссоры. Снова пришли числа к нолю.

Задумался ноль. Как разрешить проблему? Думал, думал, да и придумал. Чтобы отрицательные числа отличались, ставить перед ними знак минус.

И восстановился в числовом царстве мир. Так и живут теперь дружно на одной улице Числовой прямой слева от ноля отрицательные числа, а справа – положительные.

Кто больше?

Мирон живут числа на Числовой прямой. Отрицательные совсем исправились, поведение только отличное. Но иногда между собой поспорят. Вот однажды к числу -1 в гости пришло число -7. Разговаривали, чай пили и заспорили, кто из них больше. -7 говорит: «Конечно же, я. Ведь я семь, а ты всего лишь один». А -1 не уступает: «И что же, а я к положительным числам ближе. А они даже ноля больше, значит и я больше». Спорили-спорили и снова пошли к мудрому нолю. Ноль видит проблема не только этих, а всех отрицательных чисел. Подумал и решил так: отрицательные числа живут на числовой прямой меньше, чем натуральные, пусть и будут они меньше любого положительного числа и ноля. Получилось, какое число правее, то и больше. Поэтому -1 больше -7. Обнялись числа, и пошли чай допивать.

А если какой шестиклассник по ошибке запишет, что -7 больше -1, числа хором закричат: «То больше, которое правее».

Игры Добро Воли

Числа никогда не скучали. То маскарад устроят, то спортивные соревнования. Сначала соревновались числа -2 и 2. Кто быстрее до домика ноля добежит? Прибежали одновременно. Вышли на старт -8 и 8. Бегут, из сил выбиваются, но пришли к финишу одновременно. Задумались числа и заметили, что соревновались числа схожие, только одно положительное, а другое отрицательное. Словно одно зеркальное отражение другого. И живут на одинаковом расстоянии от домика ноля. Назвали их противоположными.

Стали противоположные числа канат тянуть. Тянут-тянут, а с места сойти не могут. Опять загадка. Получается – модули их равны, а сумма равна нолю.

Решили числа другие суммы посчитать. Вышли числа -5 и 3. Число -5 в миг 3 перетянуло на 2, получилось -2. Вышли -3 и 5, и число 5 перетянуло на 2, получилось 2. Потом числа догадались, как узнать, какое число перетянет и на сколько (а Вы догадались?). Стали соревноваться в скорости, кто быстрее сумму вычислит.

Что в результате? Математические сказки помогли активизировать деятельность учащихся с неустойчивым вниманием, пониженным интересом к предмету, сделали изучение сложной темы интересным и занимательным процессом. Самые пассивные дети эмоционально реагировали на сказки. Сказки, сочиненные учителем, помогли учащимся раскрыть свой творческий потенциал, попробовать свои силы в сочинительстве. Появились ученические математические сказки. Возможно несовершенные, но искренние, раскрывающие учителю внутренний мир ребенка.

Сказки по математике, составленные учениками

«Как появился знак «=»»?

В одном городке под названием «Цифрополис» жили – были числа. А числа там жили самые разные. И они очень любили складываться, вычитаться, умножаться и делиться. Но вот беда! Они всегда забывали, какое произведение, разность, частное или сумма от этого получалась. На бумаге они могли записать лишь само действие, а сколько получится – нет. Ведь не было специального знака. Тогда цифры пошли к королеве Математике. И королева Математика дала им для вычислений знак «=». Отныне стой поры цифры любят, уважают и ценят этот знак!

«Самая маленькая, но в то же время самая большая цифра»

Жила – была цифра 0 и все остальные цифры над ней смеялись, даже 1 над ней часто смеялась. «Да что же ты можешь? Ты же просто пустое место», - говорила 8. «Вот увидите! Если я есть, то для чего-нибудь буду нужна», - обиженно отвечала цифра 0.

Нуль убежал прочь, а все остальные очень долго смеялись. Нулю было ужасно обидно, что всеми цифрами можно что-то подсчитать, а им ничего. У нуля испортилось настроение.

Но вот в один прекрасный момент нуль подошёл ко всем цифрам, его как всегда встречали усмешками. Но тут он улыбнулся и сказал: «А вот прежде чем смеяться, давайте я встану позади кого-нибудь из вас». «Ну, давай», - согласилась 5. Нуль встал позади 5 и все цифры пришли в изумление, увидев, что 5 превратилась в 50. И теперь то цифры поняли, что без 0, самой маленькой цифры, они остаются просто цифрами, а с 0 они становятся в 10 раз больше!

«Числитель и знаменатель»

Жили-были в одном королевстве «Математика» два друга: числитель и знаменатель. Как-то раз у них возник спор: «Кто должен стоять первым ?» Долго они не могли решить этот спор и решили они отправиться во дворец. Добрались они до дворца и обратились к королеве. Они всё рассказали ей. И королева им сказала, что дроби не получится, если не будет числителя или знаменателя. Королева расставила их по местам: числителя сверху, а знаменателя снизу, но ничего не получилось – чего-то не хватало. И королева вспомнила, что не хватает дробной черты. Королева познакомила друзей с дробной чертой. И они попробовали снова и у них всё получилось: числитель вверху, знаменатель внизу, а между ними дробная черта. И так они больше никогда не ссорились и жили вместе с дробной чертой.

«Сказка»

Жили-были квадрат, прямоугольник, круг, треугольник, задачка и пример. И вот они начали спорить. Фигуры говорят, что они главные, а задачка и пример, что они. Фигуры говорят, что мы главные, потому что из нас могут выйти новые фигуры. А задача и пример хором сказали, что мы всё равно главнее, потому что без нас человек не смог бы считать.

Тут они поссорились и больше не общались. Фигуры ушли в царство геометрии, а задача и пример ушли в царство алгебры. Вот так появилась алгебра и геометрия!

Математика и грамматика.

Жили-были Математика и грамматика. Математика стала хвастаться:

-Я лучше всех и главнее всех! Меня используют везде: и в быту, и при строительстве, и при расчетах!

-Неправда! – отвечает ей Грамматика. – Мы обе нужны!

-Нет! Я нужнее! – топнула ногой Математика.

-Мы обе важны и нудны! – спорит Грамматика с Математикой.

Поссорились лучшие подруги и разошлись. А Грамматика решила проучить Математику, чтобы та не зазнавалась. Собралась и пошла она к знакомому Магу. Пришла Грамматика к волшебнику и говорит:

-Я хочу проучить Математику, чтобы та не зазнавалась. Помоги мне это сделать.

-Хорошо! – отвечает Маг.

И волшебник сделал так, чтобы все забыли Математику. Никто не считал, дома не строились. Все стали жить без Математики, считая, что для жизни уже все есть. А Грамматику уважали. Люди стали писать стихи, рассказы, повести.

Пожили люди так без Математики – дома не строятся, магазины не работают. Плохо без Математики! Грамматика тоже заскучала без своей подруги, да и поняла она, что без Математики плохо на свете.

Пошла снова Грамматика к знакомому Магу и просит:

-Верни все на свои места. Плохо без моей подруги Математики, я была не права!

-Хорошо! - улыбнулся Маг. – Иди домой. Я все сделаю. Только в следующий раз, если ты захочешь, что-нибудь изменить в жизни хорошенько подумай!

Пришла Грамматика к Математике и увидела свою грустную подругу. Рассказала Грамматика Математике, как она поступила.

-Я оказалась не права – закончила свой рассказ Грамматика. – Ты тоже очень важна! И прежде, что-нибудь изменить что-то в этой жизни я хорошенько подумаю!

И Математика с Грамматикой больше никогда не ссорились.

Вывод из этой сказки таков: Математика и Грамматика нужны всегда в жизни.

Занятия 29-34. Проектная деятельность.

Темы проектов:

1. Колыбельные, в которых встречаются числа.

2. Составление математических сказок.

3. Составление задач на краеведческую тему по Нюксенскому району.