Казённое общеобразовательное учреждение Омской области

«Адаптивная школа – интернат №15»

Конспект урока геометрии по теме:

«Площадь треугольника»

8 класс

(II отделение со слуховой депривацией)

Составитель: учитель

высшей квалификационной категории

Свиркова Людмила Васильевна

Омск 2018г.

Урок разработан и апробирован для учащихся 8 класса, II отделения со слуховой депривацией.

План-конспект урока по геометрии

Тема: Площадь треугольника

Учитель: Свиркова Людмила Васильевна, учитель математики, высшая категория

Предмет: геометрия

Класс: 8 (2 отделение)

Учебник: УМК «Геометрия 7 – 9 классы». Л.С. Атанасян, В.Ф. Бутузов, С.Б.Кадомцев и др., Москва, Просвещение, 2010 г

Тип урока: Урок открытия новых знаний, обретения новых умений и навыков

Вид урока: Урок - практикум

Цели урока: 

Деятельностная: научить детей новым способам нахождения знаний, ввести новые понятия, термины.

Содержательная: сформировать систему новых понятий, расширить знания обучающихся за счёт включения новых определений, терминов, описаний.

Задачи урока:

Образовательные:

- актуализировать знания;

- систематизировать знания;

- проконтролировать усвоение знаний.

Воспитательные:

- формировать культуру речи учащихся;

-воспитывать самостоятельность, уверенность, чувство собственного достоинства.

Развивающие:

- развивать память, речь, мышление, наблюдательность, умение анализировать, сопоставлять, формулировать выводы;

- совершенствовать навыки решения задач;

- развивать познавательный интерес, уверенность в своих силах.

Коррекционные:

- осуществлять коррекцию произносительных навыков в процессе чтения формул и правил, материала из учебника и с доски.

Методы обучения: использование ИКТ, метод исследования, технология развивающего обучения, технология деятельностного подхода, фронтальная беседа, фронтальный опрос.

Оборудование и средства обучения: компьютер, проектор, экран, учебник «Геометрия 7-9», Л.С. Атанасян. и др., рабочие тетради, меловая доска, набор чертежных инструментов.

Планируемые результаты:

Предметные:

- ученик научится находить площадь треугольника;

- ученик получит возможность применять знания при решении задач с практическим содержанием.

Метапредметные:

- ученик научится давать определения понятиям, обобщать, устанавливать аналогии с известными правилами;

- ученик получит возможность научиться элементам волевой саморегуляции, мобилизации сил к преодолению препятствий

Личностные:
- ученик получит возможность контролировать процесс и результат учебной и математической деятельности;

- ученик получит положительный опыт работы в парах и группах.

Основные виды деятельности: решение проблемы, устная работа, работа в парах, работа в группах, взаимопроверка, хоровое проговаривание, работа на голое ухо, речевой треугольник, индивидуальная работа, самооценка, взаимооценка, рефлексия.

Ход урока

Слайд 1 (Сл.)

Тема: "Площадь треугольника"

I.Организационный этап. (работа за экраном – р/э) – коррекционная работа (к/р.)

Учитель: Здравствуйте, я рада вас видеть. Кто сегодня дежурный?

Кого нет в классе? У всех аппараты? Все меня слышат хорошо? (Если нет, то пересадить учащихся). Денис, спроси у Жени: Какой сегодня дежурный звук? Назовите тему урока. (Ц – С). – (речевой треугольник – р/т) - к/р. Следим за звуками, говорим правильно.

Проверьте свою готовность к уроку: тетрадь, учебник, ручка, карандаш, линейка и, конечно, хорошее настроение.

Сл.2

В конце урока нужно будет оценить свою работу и работу своих товарищей по критериям: знание правил, умение пользоваться формулами, решение задач, самостоятельная работа, правильное произношение и соблюдение правил орфоэпии. Правильно выполненное задание -2 балла, допущена ошибка – 1 балл, неправильно выполненное задание или невыполненное – 0 баллов.

10 баллов – отметка «5», 9-8 баллов –отметка «4»,

7-6 баллов – отметка «3», 5 и менее баллов – отметка «2».

Повторите, как оценить свою работу и работу товарища на уроке. (Спросить 2-3 учащихся).

II. Актуализация знаний.

Учитель: Площади каких фигур мы уже умеем находить? - (р/э) - к/р.

(Площадь прямоугольника, квадрата, параллелограмма, ромба.)

Сегодня нам предстоит повторить все, что изучили о площадях известных фигур: о прямоугольнике, квадрате, параллелограмме, ромбе; вывести формулу для площади треугольника, научиться решать задачи.

Запишите соответствующие формулы прямоугольника, квадрата, параллелограмма и ромба в тетрадь.

1 ученик у доски выполняет задание: продолжить запись формулы.- (раб. на голое ухо- (г/у)) – к/р.

Проверяем: S = a•b,  S = a²,  S = a•h.

Сл.3

Повторим словарь, который нам будет нужен на уроке (можно использовать конспекты прошлых уроков): хором - к/р.

Квадрàт, а - сторонà квадрàта,

Прямоугòльник, а - длинà, в - ширинà ,

Смèжные стòроны,

Параллелогрàмм, ромб, а, в (бэ) - основàния,

Н,h (аш) - высотà,

S (эс) - плòщадь.

Назовите единицы измерения площадей. (Работают парами, называя друг другу единùцы площадèй).

(Единùцы площадèй: квадрàтный миллимèтр, квадрàтный сантимèтр, квадрàтный децимèтр, квадрàтный метр, квадрàтный киломèтр, ар, гектàр) (хором) - к/р.

Записываем: мм², см ²_, дм² , м ², км ², а, га.

Сл.4

Устная работа:

Учитель: Найдите площади фигур, изображенных на экране. Задание выполняем в группах. (Учащиеся делятся на 2 группы.)

Какая группа выполнит задание правильно и быстрее?

Обоснуйте применение формул (рассказать правило).

Учитель. Какое правило вы использовали для нахождения площади многоугольника?

(Площадь многоугольника равна сумме площадей фигур, на которые его можно разбить.)

Учитель: Почему не получилось найти площадь фигуры № 4, используя это правило?

(В разбиении фигуры присутствует треугольник, а площадь треугольника мы находить не умеем.)

Учитель: Таким образом, у нас возникла проблема, исходя из нее, сформулируйте тему урока, запишите её.

Учитель: Тема нашего урока очень важна, т.к. любую геометрическую фигуру можно разбить на конечное число треугольников, и если вы будете знать способ нахождения площади треугольника, то сможете найти площадь любой геометрической фигуры.

Какую цель мы поставим перед собой? 

Сл.5

Ученик: Вывести формулу площади треугольника, доказать ее, научиться применять её при решении задач (хором) – к/р.

Сл.6 -7

Учитель: Треугольник – одна из магических фигур, с которой мы очень часто встречаемся в нашей жизни.

Крыши старых деревянных домов и современных многоэтажных домов имеют форму треугольника. Это связано с тем, что на таких крышах не задерживается талый снег и легко стекает дождевая вода.

Различные головные уборы: треуголки, пилотки, колпаки, косынки – имеют треугольную форму. Треуголка – форменный головной убор.

Сейчас письма мы отправляем в прямоугольных конвертах, а раньше, во время войны, письма имели треугольную форму. Солдатский треугольник – письмо без марки и конверта, отправленное солдатом с фронта или солдату на фронт. Во многих семьях до сих пор хранят такие письма.

В железнодорожном транспорте также встречаются треугольники. На фотографиях изображены крепления спальных мест и багажных полок и т.д.

Как вы думаете, почему? (Треугольник – одна из самых прочных, экономичных фигур). Правильно.

III. Изучение нового материала:

Сл.8 - 9

Учитель: Решим задачу №1: Смежные стороны параллелограмма АВСД, равные 8 см и 12 см, образуют угол 30⁰. Найдите площади треугольников АВС и АВД.

К доске идёт 1 ученик, остальные решают задачу №1 самостоятельно.

Дано:

АВСД – параллелограмм,

АВ = 8 см, АД = 12 см – смежные стороны,

ﮮ А = 30^0.

Найдите: S_АВД и S_ВСД - решает ученик.

Сл.10 Проверим решение.

Решение:

1) Площадь параллелограмма равна произведению его основания на высоту.

2) Проведём диагональ ВД и высоту ВН. Треугольник АВН- прямоугольный. 3) S_АВСД. =АД х ВН.

4) ВН = = = 4 (см) – катет, лежащий против угла 30^0., равен половине гипотенузы.

5) S_АВСД = 12 х 4 = 48 (см²)

6) S_АВД = S_ВСД. = 48 : 2 = 24 (см²), т.к. диагональ делит параллелограмм пополам.

Ответ: площади треугольников АВС и АВД равны 24 квадратным сантиметрам.

Индивидуальное задание для слабоуспевающих обучающихся (карточка). Задача № 2: Основание и высота параллелограмма АВСД равны 12 см и 8 см. Найдите площади треугольников АВС и АВД (учитель работает с каждым учащимся индивидуально) - к/р.

Дано:

АВСД – параллелограмм,

АД = 12 см – основание, ВН = 8 см – высота;

Найдите: S_АВД и S_ВСД.

Решение:

1) Проведём диагональ ВД и высоту ВН.

2) Площадь параллелограмма равна произведению его основания на высоту.

S_АВСД. =АД х ВН = 12 х 4 = 48 (см²)

3) S_АВД = S_ВСД. = 48 : 2 = 24 (см²), т.к. диагональ делит параллелограмм пополам.

Ответ: площади треугольников АВС и АВД равны 24 квадратным сантиметрам.

Сл.11

Итак, сделаем вывод: площадь треугольника равна половине площади параллелограмма.

А т.к., площадь параллелограмма равна произведению его основания на высоту, то  площадь треугольника равна половине произведения его основания на высоту.

Запишем данное утверждение в тетрадь и докажем данную теорему.

Сл.12

Учащиеся доказывают теорему самостоятельно. Учитель акцентирует внимание на то, что треугольник надо достроить до параллелограмма и доказать равенство получившихся треугольников.

Дано:

АВС-треугольник,

АВ - основание треугольника,

Проведём высоту СН

S - площадь треугольника.

Доказать, что S_АВС = АВ х СН.

Сл.13 Проверим доказательство.

Доказательство:

1. Достроим треугольник АВС до параллелограмма АВСД.

2. Треугольники АВС = ВСД (АВ = СД и АС = ВД – противоположные стороны параллелограмма равны, ВС – общая сторона, по третьему признаку равенства треугольников).

3. Следовательно, площадь треугольника АВС равна половине площади

параллелограмма АВСД, т.е. S_АВС = АВ х СН. Теорема доказана. (Проверяем доказательство по презентации).

Сл.14 - 15

Минута релаксации - (минута отдыха)

IV. Углубление и закрепление полученных знаний:

Учитель: Вспомним о понятии прямоугольных треугольниках. Это, действительно, отдельный класс треугольников и поэтому площадь их находится особым образом.

Рассмотрим прямоугольный треугольник АВС. Как найти его площадь? Что выбрать за основание, а что - за высоту? Постарайтесь самостоятельно сформулировать утверждение - (сделать заранее чертёж).

Запишем следствия:

Сл.15

Следствие 1: Площадь прямоугольного треугольника равна половине произведения его катетов.

Следствие 2: Если высоты двух треугольников равны, то их площади относятся как основания.

Учитель: Можем ли мы теперь вернутся к задаче, которую мы не решили в начале урока, и решить её? Давайте решим её вместе.

(Для смены зрительного восприятия чертеж к этому блоку сделать на обычной доске заранее. Задача № 4 из устной работы.)

Рассмотрим фигуру. Эта фигура состоит из прямоугольника и прямоугольного треугольника.

Решение:

1) 11 х 8 = 88 (кв.ед.) – площадь прямоугольника,

2) катеты прямоугольного треугольника: 11 и 10 – 8 = 2,

3) (11 х 2) = 11 (кв.ед.) – площадь прямоугольного треугольника,

4) 88 + 11 = 99 (кв.ед.) – площадь всей фигуры.

Ответ: 99 квадратных единиц.

Учитель: Работаем с учебником. (Задача на следствие № 1)

Откройте учебник на странице 128, задача №471 (а), прочитайте задачу. Если всё ли понятно? Решайте самостоятельно.

В это время учитель работает индивидуально с каждым (р/г) –– к/р.

Проверяем ответ у соседа. - (взаимопроверка).

Задача на следствие № 2 (составила сама). В треугольниках АВС и А₁В₁С₁ высоты равны, основания АС = 10 дм, А₁С₁ = 5 дм, площадь треугольника АВС = 50 дм². Найдите площадь другого треугольника. (Решает задачу учитель устно, привлекая учащихся.)

Составим пропорцию: = ; 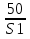= ; S₁ = = 25 (дм²);

V. Итог урока.

Учитель: Мы плодотворно работали на сегодняшнем уроке, давайте подведем итог.

- Что мы делали сегодня на уроке?

- Какую теорему доказывали?

- Повторим, чему равна площадь треугольника?

Оцените свою работу и работу товарищей на уроке с помощью критериев, которые вы видите на слайде №2. (Сл.2)

Сл.16

Рефлексия:

- Что нового вы узнали на уроке?

- Чем интересен был урок?

- Что больше всего запомнилось?

Сл.17

VI. Домашнее задание:

Запишите домашнее задание: выучить теорему и следствия, используя конспекты и методические пособия, книги; решить задачи № 468(а), № 471 (б).

Спасибо за сотрудничество, спасибо за урок.

Литература:

1. Л.С. Атанасян, В.Ф. Бутузов, С.Б.Кадомцев и др., «Геометрия 7-9 классы». Москва, Просвещение, 2010 г.

2. Л.С. Атанасян, В.Ф. Бутузов, С.Б.Кадомцев и др. Изучение геометрии 7 – 9. Методические рекомендации к учебнику. Москва, Просвещение, 2009 г.

3.Т.А.Бурмистрова. Программы общеобразовательных учреждений. «Геометрия 7-9 классы», Москва, Просвещение, 2010 г.

4. Б.Г. Зив, В.М. Мейлер. Дидактические материалы по геометрии. Москва, Просвещение, 2007 г.

5. А.А.Окунев, Л.П. Евстафьева, Т.Г. Ходог и др. Геометрия. Книга для учителя. Санкт – Петербург, «Специальная Литература», 2008 г.