Приложение 1.

О Пифагоре.

Вопросы: 1) Когда и где родился, кто родители? Каким он был в детстве?

2) Пифагор в Египте

3) Вавилонская школа

4) Тайная школа «Великая Греция»

5) Особенности поведения Пифагора

6) Пифагор, его увлечения.

Великий ученый Пифагор родился около 570 г. до н.э. на острове Самосе. Отцом Пифагора был Мнесарх, резчик по драгоценным камням. Имя же матери Пифагора неизвестно. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности, и когда подрос, неугомонному воображению юноши стало тесно на маленьком острове. Пифагор перебрался в город Милеет и стал учеником Фалеса, которому в то время шёл восьмой десяток. Мудрый учёный посоветовал юноше отправиться в Египет, где сам, когда-то изучал науки.

Перед Пифагором открылась неизвестная страна. Его поразило то, что в родной Греции боги были в образе людей, а египетские боги - в образе полулюдей-полуживотных. Знания были сосредоточены в храмах, доступ в которые был ограничен. Пифагору потребовались годы, чтобы глубоко изучить египетскую культуру прежде, чем, ему было разрешено познакомиться с многовековыми достижениями египетской науки.

Когда Пифагор постиг науку египетских жрецов, то засобирался домой, чтобы там создать свою школу. Жрецы, не желавшие распространения своих знаний за пределы храмов, не хотели его отпускать. С большим трудом ему удалось преодолеть эту преграду. Однако по дороге домой, Пифагор попал в плен и оказался в Вавилоне. Вавилоняне ценили умных людей, поэтому он нашёл своё место среди вавилонских мудрецов. Наука Вавилона была более развитой, нежели египетская. Наиболее поразительными были успехи алгебры. Вавилоняне изобрели и применяли при сёте позиционную систему счисления, умели решать линейные, квадратные и некоторые виды кубических уравнений.

Пифагор прожил в Вавилоне около десяти лет и в сорокалетнем возрасте вернулся на родину. Но на острове Самос он оставался недолго. В знак протеста против тирана Поликрата, который тогда правил островом, поселился в одной из греческих колоний Южной Италии в городе Кротоне. В результате первой же прочитанной лекции Пифагор приобрел 2000 учеников, которые не вернулись домой, а вместе со своими женами и детьми образовали громадную школу и создали государство, названное «Великая Греция», в основу которого были положено законы и правила Пифагора, почитаемые как божественные заповеди. В этот союз принимались с большими церемониями после долгих испытаний. Каждый вступающий отрекался от своего имущества и давал клятву хранить в тайне учения основателя. Пифагорейцы, как их позднее стали называть, занимались математикой, философией, естественными науками. В школе существовал декрет, по которому авторство всех математических работ приписывалось учителю.

Пифагор был первым, кто назвал свои рассуждения о смысле жизни философией (любомудрием).

Он был склонен к мистификациям и демонстративности  в поведении (однажды Пифагор спрятался под землей, а обо всем происходящем узнавал от матери. Потом, иссохший, как скелет, он заявил в народном собрании, что был в Аиде, и показал удивительную осведомленность о земных событиях. За это растроганные жители признали его богом).

Никогда не плакал и вообще был недоступен страстям и волнению.

 Известно также, что кроме духовного и нравственного развития учеников Пифагора заботило их физическое развитие. Он не только сам участвовал в Олимпийских играх и два раза побеждал в кулачных боях, но и воспитал плеяду великих олимпийцев. Около сорока лет учёный посвятил созданной им школе и, по одной из версий, в возрасте восьмидесяти лет Пифагор был убит в уличной схватке во время народного восстания. После его смерти ученики окружили имя своего учителя множеством легенд.

Приложение 2.

История открытия теоремы Пифагора

1) Исторические сведения из Древнего Китая, Индии, Египта.

2) Исторические сведения из Вавилона

3) Роль Пифагора

4) Формулировка теоремы

5) Запись данных, рисунка.

6) Приведение доказательства.

Теорема Пифагора.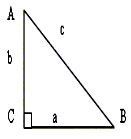

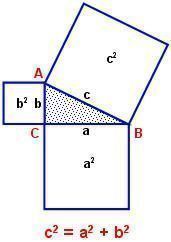
“В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов”.

Рассмотрим прямоугольный треугольник с катетами а,b и гипотенузой с.

Докажем: a²+b²=c².

Доказательство:

Достроим треугольник до квадрата со стороной a+b так, как показано на рисунке. Площадь S этого квадрата равна (a+b)². С другой стороны, этот квадрат составлен из четырех равных прямоугольных треугольников, площадь каждого из которых равна ab, и квадрата со стороной с, поэтому.

Таким образом (a+b)²= 2ab+c²

Из формулы сокращенного умножения

a²+2ab+b²=2ab+c².

a²+b²=c².

Таким образом, теорема доказана.

Приложение 3.

Применение теоремы Пифагора.

1) Как в стихотворной форме звучит теорема Пифагора.

2) Почему теорему Пифагора называли «мостом ослов»?

3) Откуда у теоремы Пифагора появилось название «теорема невесты»?

4) «Пифагоровы штаны во все стороны равны»

5) Решение задачи индийского математика 12 века Бхаскары.

6) Какой треугольник получил название египетского?

Мысль — превыше всего между людьми на земле.

Пифагор

Стихотворение о теореме Пифагора

Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдём:
Катеты в квадрат возводим,
Сумму степеней находим
И таким простым путём
К результату мы придём.

Во Франции и некоторых областях Германии в средневековье теорему Пифагора называли "мостом ослов".

Доказательство теоремы Пифагора считалось в кругах учащихся средних веков очень трудным и называлось иногда «ослиным мостом» или «бегством убогих», т.е. некоторые слабые ученики бежали от геометрии, не пытаясь понять, а зазубривая доказательство. «Ослиный мост» - непроходимый мост.

Греки же называли тех, кто не мог без посторонней помощи доказать простую теорему, профанами или просто ослами. Поэтому не удивительно, что саму теорему, которая широко использовалась в прикладных науках, в том числе и для разметки полей или строительства пирамид, древние греки называли «мостом ослов». А они очень хорошо знали египетскую математику. Что касается «моста ослов», то есть это был тот порог, который глупые люди не могли осилить, то меткие выражения, они и в наше время ценятся.

У математиков арабского Востока эта теорема получила название "теоремы невесты". Дело в том, что в некоторых списках "Начал" Евклида эта теорема называлась "теоремой нимфы" за сходство чертежа с пчелкой, бабочкой, что по-гречески называлось нимфой. Но словом этим греки называли еще некоторых богинь, а также вообще молодых женщин и невест. При переводе с греческого арабский переводчик, не обратив внимания на чертеж, перевел слово "нимфа" как "невеста", а не "бабочка". Так появилось ласковое название знаменитой теоремы-"теорема невесты".

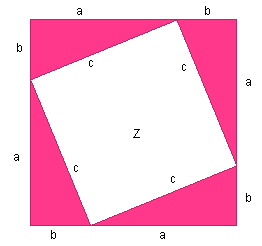
У этой теоремы есть геометрическое применение: площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на гипотенузе. Вот почему говорят: "Пифагоровы штаны на все стороны равны!". Посмотрите на эти "штаны" сами:

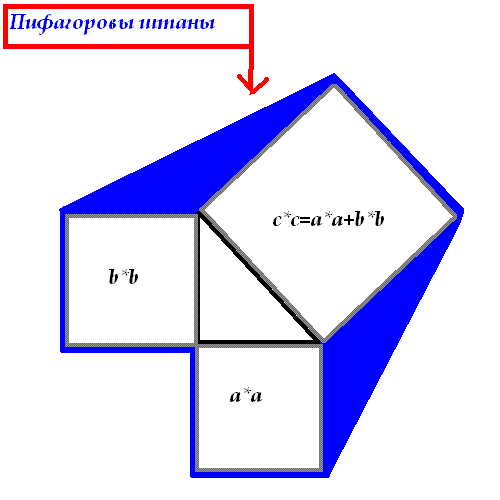
Доказать самостоятельно.

Подсказка: Рассмотреть 3 квадрата и найти их площади.

Задача индийского математика 12 века Бхаскары.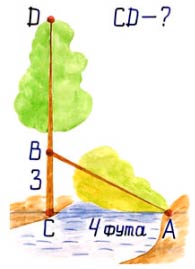

"На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в этом месте река
В четыре лишь фута была широка
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?"

Р е ш е н и е

Δ АВС – прямоугольный с гипотенузой АВ

по теореме Пифагора: АВ² = АС² + ВC²,

АВ² = 4² +3²,

АВ² = 25 ,

АВ = 5.

СD=BC+AB

CD=3+5=8

О т в е т:
СD = 8

Получили прямоугольный треугольник со сторонами 3, 4 и 5 ед. Это единственный прямоугольный треугольник, стороны которого равны трём последовательным натуральным числам. Его часто называют египетским треугольником, так как он был известен ещё древним египтянам. Они использовали этот треугольник в "правиле верёвки" для построения прямых углов при закладке зданий, храмов, алтарей…

Приложение 4.

В архитектуре и строительстве.

Вопросы:

1)Как в разных стилях строительства применяется теорема Пифагора?

2) Применение в строительстве крыш

3)Строительство громоотводов

4) Применение в строительстве антенн для мобильной связи.

5) Задача из задачника Леонтия Магницкого.

Окна

В зданиях романского и готического стиля верхние части окон расчленяются на части, что не только играет роль орнамента, но и способствует прочности окон. На рисунке представлен простой пример такого окна в готическом стиле. Для того чтобы вычислить , чему равен радиус маленькой окружности (зная величины R и r)необходимо применить теорему Пифагора для выделенного треугольника.

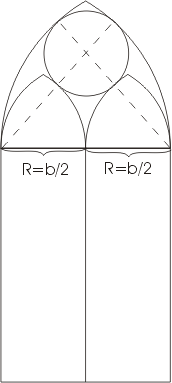
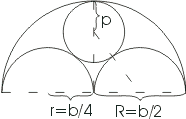
В романской архитектуре часто встречается мотив, представленный на рисунке.

Строительство крыши

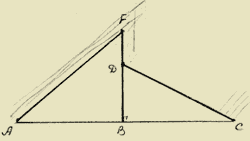
При строительстве домов и коттеджей часто встает вопрос о длине стропил для крыши, если уже изготовлены балки. Например: в доме задумано построить двускатную крышу (форма в сечении). Какой длины должны быть стропила, если изготовлены балки AC=8 м., и AB=BF.

     Решение:

     Треугольник ADC - равнобедренный AB=BC=4 м., BF=4 м. Если предположить, что FD=1,5 м., тогда:

А) Из треугольника DBC DB=2,5 м

     Б) Из треугольника ABF:

      AF==м

Ответ: 5,7 м

Также если рассматривать пирамиду как крышу дома, то, во- первых, можно рассчитать какой длины нужно сделать боковые ребра, чтобы при данной площади чердака была выдержана высота крыши.

Во- вторых, решить вопрос о величине боковой поверхности при подсчете стоимости кровельных работ.

Молниеотвод

Молниеотвод защищает от молнии все предметы, расстояние до которых от его основания не превышает его удвоенной высоты. Определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту.
Решение:
По теореме Пифагора h² ≥ a²+b², значит h ≥ (a²+b²)^½.
Ответ: h ≥ (a²+b²)^½

Мобильная связь

В настоящее время на рынке мобильной связи идет большая конкуренция среди операторов. Чем надежнее связь, чем больше зона покрытия, тем больше потребителей у оператора. При строительстве вышки (антенны) часто приходится решать задачу: какую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе (например радиусе R=200 км?, если известно. что радиус Земли равен 6380 км.)
Решение:
Пусть AB= x, BC=R=200 км, OC= r =6380 км.
OB = OA + AB
OB = r + x
Используя теорему Пифагора, получим ответ.
Ответ: 2,3 км.

Задача из задачника Леонтия Магницкого (18 век)

"Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп.

И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать."

ВС²=125²-117² = (125-117)(125+117)=8*242=4*2*121*2

ВС=2*2*11=44 стопы

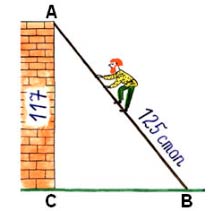
Ответ: 44 стопы.

Урок по теме «Теорема Пифагора» (Презентация слайд 1)

Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора…

Иоганн Кеплер (Презентация слайд 2)

Учитель: Наверное, вы уже слышали имя Пифагора, слышали о том, что существует такая теорема.

Давайте попробуем сформулировать, чем мы будем сегодня на уроке заниматься, то есть поставим цели нашего урока.

Цели: 1)Более подробно узнать, кто такой Пифагор (обобщить и систематизировать

знания о Пифагоре)

2)Узнать о теореме Пифагора (показать исторические истоки теоремы)

3) Узнать, где эта теорема применяется (научить учащихся применять полученные

знания к решению прикладных задач);

4) Развить самостоятельность и познавательный интерес в изучении геометрии.

Учитель: Открываем тетради, записываем число и сегодняшнюю тему урока.

А я расскажу, как мы будем работать на уроке.

Задачи: 1) Помогать учащимся в формировании умений и навыков работы с дополнительной информацией, умений обобщать и самостоятельно делать выводы.

2) Продолжить формировать навыки анализа, умения строить доказательства при изучении теоремы.

3) Помогать учащимся в нахождении значений применяемости теоремы для человечества в быту, строительстве в разные эпохи существования человечества.

4) Воспитывать эстетический вкус у учащихся через восприятие картин и красоты восприятия текстов задач жителей древнего мира;

5) Помогать в развитии у учащихся познавательного интереса к изучению геометрии;

5) Продолжить формирование умений представлять результаты своей работы.

Основные этапы урока:

1) Повторение

2) Изучение нового материала

3) Закрепление

4) Итог

5) Рефлексия в форме письменной работы (8 вопросов тестовых и 2 требуют подробного ответа).

Сначала разобьем класс на 4 группы:

Историки, Теоретики, Практики и Архитекторы.(на столы необходимо приготовить таблички с названиями групп)

I) Повторение.

Прежде чем начать изучать новую тему, давайте повторим пройденный материал.

Вопросы:

А)

1) Почему прямоугольный треугольник имеет такое название.

2) Как называются стороны в прямоугольном треугольнике. (презентация ( слайд 2))

3) Что представляет собой квадрат.

Учащиеся отвечают на вопросы.

Б)

Работа с сигнальными карточками (зеленая и красная)

На доске:

а) а² б) a+b ; в) г) a·b

Учитель задает вопрос, называет варианты ответов, учащиеся показывают карточки

1) Чему равна площадь прямоугольного треугольника,

2) Чему равна площадь квадрата.

II) Изучение нового материала

Работа методом «кейса» по группам

Для этого каждой группе раздается текст и вопросы ( см. Приложение 1,2,3,4) . Каждому члену группы раздается одинаковый текст. Учащиеся обсуждают, кто ищет ответ на определенный вопрос, который потом будут рассказывать. Работают в группах минут 7-10.

В это время можно часть выступлений оформить на досках.

Далее следуют выступления групп.

1)О Пифагоре (выступление группы Историков, см. Приложение 1)

После выступления учащихся, учитель дополняет выступление с демонстрацией слайдов презентации ( 3,4,5,6 ) о роли науки в древние времени, о том, какое почетное место в обществе занимали ученые люди.

2) История открытия теоремы Пифагора (выступление группы Теоретиков, см. Приложение 2).

Для этого учащиеся выносят на доску доказательство теоремы.

После выступления учащихся учитель просит учащихся записать в тетрадь теорему, доказательство, и в рамочку выделить формулу

с2=а2+b2

Также учитель говорит, что найдено более 100 доказательств этой теоремы. А в фильме «Приключение Электроника» Электроник доказывал эту теорему 25 способами. И в домашнем задании вам надо будет отыскать несколько доказательств.

3) Применение теоремы Пифагора (выступление группы Практиков, см. приложение 3)

Для выступления учащиеся выносят на доску рисунок «пифагоровых штанов», самостоятельное доказательство равенства площадей, решение задачи про дерево.

Учитель во время выступления учащихся показывает слайды 7,8. И для задачи 9 слайд.

После выступления учитель просит учащихся записать в тетрадь доказательство и решение задачи.

4) В архитектуре и строительстве (выступление группы Архитекторов, см. приложение 4)

Для выступления на доску выносится рисунок ската крыши, записывается решение задачи про крышу, записывается решение задачи из задачника Магницкого.

Учитель во время выступления демонстрирует слайды 10, 11,12. И для объяснения решения задачи из задачника Магницкого – слайд 13.

После выступления учащихся учитель простит написать применение теоремы: 1) в строительстве крыш; 2) в строительстве окон романского и готического стиля; 3) в строительстве громоотводов; 4) в строительстве антенн для мобильной связи.

А также перенести в тетрадь решение задачи из задачника Магницкого.

Физкультминутка ( слайд 14 Презентации)

Далее учитель говорит о том, что теорема Пифагора также применяется в литературе, мобильной связи, архитектуре (индийцы, например, использовали её для построения алтарей, которые по священному предписанию должны иметь геометрическую форму, ориентированную относительно четырех сторон горизонта), а также в астрономии. В конце 19 века высказывались разнообразные предположения о существовании обитателей Марса подобных человеку. Вопрос о том, можно ли с помощью световых сигналов объясняться с этими гипотетическими существами, вызвал оживленную дискуссию. Парижской академией наук была даже установлена премия в 100000 франков тому, кто первый установит связь с каким-нибудь обитателем другого небесного тела; эта премия все еще ждет счастливца. В шутку, хотя и не совсем безосновательно, было решено передать обитателям Марса сигнал в виде теоремы Пифагора. Неизвестно, как это сделать, но очевидно, что математический факт, выражаемый теоремой Пифагора имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.

Даже глубину водоема можно определить, используя теорему Пифагора. Рассмотрим древнюю китайскую задачу. Для объяснения учитель использует слайд 15 из Презентации.

III. Закрепление.

Задача из китайской "Математика в девяти книгах"

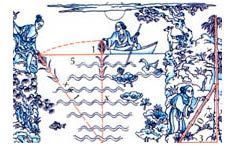
"Имеется водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его.

Спрашивается: какова глубина воды и какова длина камыша?"

Прямоугольный треугольник АВС, <С=90⁰, АС=5 чи, СB=h=x; АВ=х+1.

АВ²=АС²+ВС²

(х+1)²=5²+х²

х²+2х+1=25+х²

2х=24

х=12 (чи)- глубина водоема

х+1=13 (чи)- длина камыша.

Ответ: 12 чи- глубина водоема, 13 чи- длина камыша.

IV. Итог.

А теперь давайте, прежде чем приступить к проверочной работе подведем итог, что мы сегодня узнали

1) Когда и где жил Пифагор? Что интересного про него можно сказать?

2) Чем он знаменит?

3) Как звучит теорема Пифагора?

4) Почему эту теорему называли «теоремой невесты»?

5) Почему эту теорему называли «мостиком ослов»?

6) Где применяли и применяют эту теорему?

Молодцы!!!

А теперь записываем домашнее задание.

Домашнее задание: Оформить в виде доклада не более 3 доказательств теоремы Пифагора (в которых вы смогли разобраться), решить задачу и сделать к ней красивый рисунок, определить, к какой стране относится эта задача.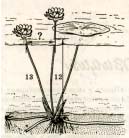

Задача выдается каждому учащемуся на карточке (можно без рисунка) .

Задание можно выдать, когда ученики будут писать проверочную работу.

Задача. “На глубине 12 футов растет лотос с 13-футовым стеблем . Определите, на какое расстояние цветок может отклониться от вертикали, проходящей через точку крепления стебля ко дну”.

V. Рефлексия.

Приступаем к проверочной работе.

(учащиеся могут прямо на выданном листе обводить карандашом правильные ответы, а на 2 последних задания – писать там же)

Если есть возможность проведения урока в компьютером классе, то проверочную работу можно сделать в форме компьютерных тестов в программе «My test». Тогда учащиеся сразу увидят свои баллы. Правда, придется заменить 9 и 10 вопросы на тестовые.

Проверочная работа.

1. О каком древнем математике вы сегодня узнали

а) о Демокрите; б) о Магницком; в) о Пифагоре; г) о Ломоносове.

2. Что открыл этот математик

а) теорему; б) рукопись; в) древний храм; г) задачу.

3. Как называется большая сторона в прямоугольном треугольнике?

а) медиана; б) катет; в) биссектриса; г) гипотенуза.

4. Почему теорему назвали «теоремой невесты»

а)потому, что она была написана для невесты;

б) потому, что она была написана невестой;

в) потому, что чертеж похож на «бабочку», а «бабочка» переводится как «нимфа» или» невеста»;

г) потому, что это загадочная теорема.

5. Почему теорему назвали «мостиком ослов»

а) она применялась для дрессировки осликов;

б) только умный и упрямый мог преодолеть этот мостик и доказать эту теорему;

в) написали ее «ослики»;

г) очень сложное доказательство теоремы.

6. В теореме Пифагора квадрат гипотенузы равен

а) сумме длин сторон треугольника;

б) сумме квадратов катетов;

в) площади треугольника;

г) площади квадрата.

7. Чему равны стороны египетского треугольника?

а) 1, 2, 3; б) 3,4,5; в)2,3,4; г) 6,7,8.

8. Если в прямоугольном треугольнике два катета соответственно равны 5см и 12 см, то гипотенуза равна…

а) 15 см; б) 17 см; в) 13 см; г) 60 см.

9. Напишите, где применяется теорема Пифагора

10. Напишите, что интересного вы узнали на этом уроке.

На уроке ученики должны получить 2 оценки. Одну за работу в группе, а вторую за письменную работу. Первую оценку учитель может озвучить уже в конце урока. А вторую- на следующем.

И закончить урок я бы хотела словами Пифагора:

«Как хорошо, когда благоденствие человека основано на законах разума».

Будьте благоразумными.

Урок окончен. Всем спасибо.